离散数学与组合数学考试复习大纲

一、考试大纲

离散数学与组合数学是现代数学的重要分支,是计算机科学的基础理论课程数理逻辑、集合论、图论与代数结构是离散数学的重要组成部分。要求考生对它们的基本概念有较深入的了解,能够系统地掌握命题演算、谓词演算及朴素集合论的经典内容,掌握演绎推理的基本方法。掌握图论的基本定理和应用,熟悉代数系统的基本概念及定理。组合数学部分要求考生掌握各种基本的计数方法,线性常系数递推关系的解法,Burnside引理和Polya定理的应用,容斥原理和鸽巢原理的应用等。

主要内容包括:

(一)命题逻辑的等值演算与推理演算

1.命题逻辑的基本概念、命题逻辑联结词与真值表,重言式
2.简单命题的形式化(简单自然语句的形式化)
3.等值定理、基本等值公式以及等值演算
4·命题公式与真值表的关系、联结词的完备集)
5.析取范式、合取范式、主析取范式和主合取范式
6.命题逻辑的推理规则与推理演算,归结推理证明方法
7.命题逻辑公理系统的概念,公理系统的基本结构

(二)谓词逻辑的等值演算和推理演算

1,谓词、量词的基本概念及表示法
2.复杂自然语句的形式化
3,否定型等值式、量词分配等值式
4·范式、前束范式,Skolem标准形
5,基本推理公式及其证明方法
6,谓词逻辑的推理规则与推理演算,归结推理法

(三)集合与关系

1,集合的概念、性质和基本运算,集合间的关系和特殊集合
2,有限集合的基数,包含排斥原理
3,集合论公理系统,无穷公理和自然数集合
4,二元关系的概念、关系矩阵和关系图
5,关系的逆、合成,关系的基本性质,关系的闭包
6.等价关系和划分,偏序关系与哈斯图:
7,任意集合上的函数定义与性质、特殊函数,满射、单射与双射
8.集合的势、无限集合的基数

(四)图论的基本概念、路与回路

1.图的基本概念与性质
2.图的代数表示
3.途径、路、回路、迹的定义
4.欧拉环游(欧拉闭迹)与欧拉迹
5.汉密尔顿路与回路
6.最短路径
7.连通性
8.有向图

(五）树、平面图与图的着色

1.树的定义及等价条件
2.支撑树的计数
3.森林
4,最短树
5.平面图与极大平面图
6,对偶图
7.色数与色多项式

###（六）代数结构
1.代数系统的概念
2,同构与同态
3,群的基本知识
4.循环群、群的同构
5,变换群和置换群、Caylay定理
6.陪集和群的陪集分解、Lagrange定理
7,正规子群与商群
8.同态、同态基本定理
9.域的概念

###(七)排列与组合
1.加法法则与乘法法则
2.排列与组合
3.Stirling 近似公式
4.排列的生成算法
5.组合的生成算法
6.可重组合
7,若干等式及其组合意义

###（八)母函数与递推关系
1.母函数
2.递推关系
3.Fibonacci 列
4.线性常系数递推关系
5.整数的拆分和Ferrers图像
6.指数型母函数
7.母函数和递推关系应用举例
8,错排问题
9.Sliding数效
10.Catalan数

###（九）容斥原理和鸽巢原理
1,容斥原理
2,棋盘多项式与有限制排列
3,一般公式
4·二项式反演与Mobius反演
5.鸽巢原理
6.Ramsey问题和Ramsey数

###(十) Polya 定理
1.Burnside引理
2 Polya定理
3,母函数型的Polya定理
4.图的计数

二、复习指南

（一)命题逻辑的等值演算和推理演算

1,理解并掌握命题逻辑的基本概念,熟练掌握五个常用的命题联结词及其真值表,掌握命题与真值表的关系,以及由简单命题通过联结词构造复合命题的方法。
2,掌握重言式、永假式和可满足公式的区别与判别方法;理解命题形式化的步骤与方法,能够熟练地将简单自然语句利用命题联结词进行形式化。
3,掌握和理解命题公式等值的概念,掌握命题公式等值的判别方法。
4,熟悉基本的等值公式;对于常用的等值公式,能在理解的基础上熟记并能在等值演算中灵活使用。
5.了解联结词完备集的概念,掌握判别联结词完备集的方法,了解对偶式的基本概念。
6·理解范式的概念和范式定理,深入理解主析取范式和主合取范式的构成,能够熟练地将命题公式化成相应的主析取范式和主合取范式。
7,理解推理公式的基本结构,熟悉基本的推理公式,掌握推理公式的不同证明方法。
8.理解基本的推理规则,掌握使用推理规则进行推理演算的方法。
9,理解归结推理规则,掌握用归结推理法证明的方法。
10,了解命题逻辑的公理系统的概念和基本构成,进行定理推演的过程和方法。

(二)谓词逻辑的等值演算和推理演算

1,理解谓词、个体词、函数和量词的概念,重点解决使用谓词逻辑描述自然语句的表达问题,能够熟练地将一些复杂的自然语句进行形式化描述。
2,了解有限域下全称量词和存在量词的表示法,理解它在谓词逻辑中的重要作用。
3.了解普遍有效公式、可满足式和不可满足式的概念和划分方法,知道一阶谓词逻辑的判定问题的基本内容以及有关的主要结论。
4,理解谓词逻辑公式等值的概念,掌握否定型等值式的不同形式及其证明方法。
5.了解量词对不同联结词的分配律,掌握量词分配等值式的证明方法。
6·理解范式的概念,掌握前束范式的定义以及Skolem标准形的构成,会求谓词逻辑公式的前束范式和仅保留全称量词的前束范式。
7.熟悉谓词逻辑的基本推理公式,能够给出解释性的证明和其他推理公式正确性的判断。
8.理解谓词逻辑有关量词的四条推理规则,掌握使用推理规则进行推理演算的方法。
9·理解谓词逻辑的归结推理法的证明过程,掌握用归结法证明推理公式的方法。

(三）集合与关系

1.深入理解并掌握集合的概念和不同的表示方法,能够熟练地用谓词形式来描述集合中元素的性质;理解集合间的关系和特殊集合,熟练掌握集合的基本运算。
2,理解集合运算的性质和主要证明方法,能够用谓词演算或集合恒等式的方法证明集合的相等、包含或进行集合公式的化简。
3.了解集合基数的概念,掌握有限集合基数的计算方法,理解包含排斥原理及其具体应用。.
4,对集合论公理系统有概貌的了解,理解无穷公理以及自然数集合在集合论中的表示。
5·理解二元关系的概念,掌握关系矩阵表示法和关系图画法。深入理解关系的某些特殊性质,包括自反性、非自反性、对称性、反对称性和传递性以及它们之间的关系。
6.了解关系的闭包的定义及其性质;掌握已知关系R的自反、对称和传递闭包的构造方法。
7.深入理解等价关系和划分的概念,掌握相关的证明思路与方法。了解相容关系和覆盖的概念以及它们与等价关系和划分的主要区别。
8.深入理解偏序关系和哈斯图的概念;掌握用哈斯图表示偏序集的方法;了解拟序关系、全序关系和链等概念。
9.理解函数的定义,特别是任意集合上的函数的概念,深入理解函数的单射、满射和双射的概念。掌握从集合A到集合B构造双射函数的方法。
10,理解集合等势的概念,掌握判断集合等势的方法。了解有限集合与无限集合的严格定义,熟悉无限集合基数的记法和康托尔定理、连续统假设的内容以及目前的基本结论。

（四）图论的基本概念、路与回路

1,理解并熟练掌握图论的最基本的概念,包括图、度、简单图完全图、正则图等
2.掌握图的最基本的性质。
3,掌握图的邻接矩阵和关联矩阵表示方法以及它们各自的性质。
4,掌握有向图与无向图的途径与闭途径,路与回路,有向途径(有向链)、有向路、有向回路、有向迹与有向闭迹、连通图等的定义及性质。
5,掌握欧拉环游与欧拉迹的定义以及存在欧拉环游的充分必要条件。
6.掌握与汉密尔顿图相关的定义以及相关定理。
7.掌握图的着色的基本内容。
8,了解求图的最短路、最小树等的基本算法。

(五)树、平面图与图的着色

1,熟悉并掌握树的等价定义及基本性质。
2,掌握连通图中支撑树数目的计算方法。
3·熟悉并掌握赋权连通图中最短支撑树的Kruskal算法。
4,熟练掌握欧拉公式,了解极大平面图的有关性质。
5,掌握对偶图的定义与构造方法,学会利用对偶图求解基本问题。
6,熟悉色数的定义、有关定理和简单图形的色数计算。
7,掌握简单图形的色多项式的计算。

（六)代数结构

1,熟练掌握代数系统的基本概念,如n元运算、单位元、逆元、半群、含么半群等。
2,理解同态与同构的有关定义,并能够进行简单证明。
3,深入理解群的有关基本知识与基本定理。
4,深入理解循环群的定义及相关定理,掌握群同构概念。
5,掌握交换群、置换群概念,及轮换、对换计算,了解Cayley定理
6.掌握陪集的定义、性质及群的陪集分解,了解Lagrange定理。
7,掌握正规子群的定义和性质,了解商群。
8.了解同态核定义及同态基本定理。
9.掌握环域的定义及基本性质。

(七)排列与组合

1,熟练运用加法法则和乘法法则,运用这些法则解决各种比较简单的计数问题。在解决计数问题的过程中注意使用合理分类和模型转换的技巧。
2.熟练掌握无重排列、无重组合、可重排列、重数给定的排列、圆排列、项链排列等概念及其计数公式的推导,并能熟练运用这些概念和计数公式解决各种问题。利用重数给定的排列及其计数公式给出多项式展开的系数计算公式,并将其与不同的球放入不同的盒子,每盒球数给定的模型联系起来。
3,利用模型转换技巧解决不易直接计算的计数问题。
4,利用不同方法推导可重组合及隔位组合的计算公式。
5·利用计算公式、归纳法和建立适当的组合模型的方法证明一些基本的组合恒等式。
6,应用各种组合模型及其计数方法解决各种相关的问题。

(八)母函数与递推关系

1,掌握序列和它的母函数的关系,掌握形式幂级数的基本运算。
2,掌握根据已知具体序列的基本性质求其递推关系,再利用母函数解递推关系,得到序列的表达式的方法。
3,掌握根据Fibonaci数列的基本性质列出其递推关系,再利用母函数求解其递推关系,即给出序列的表达式的方法。掌握利用Fi-bonacci数列的递推关系,证明一些与Fibonacci数列相关的恒等式。掌握利用Fibonacci数列在优选法中的简单应用。
4.掌握利用母函数法解一般线性常系数递推关系的方法。掌握无重根、有重根和有共轭复根3种情况下求序列表达式的方法。
5.掌握整数拆分的基本概念和一些简单方法。利用Ferrer图像解决一些拆分的计数问题。掌握根据错排的定义,求错排数列的递推关系的方法及利用母函数求解错排数列的表达式的方法。掌握利用递推关系和母函数解决一些应用问题的方法。了解Stirding数的组合意义。了解用不同方法给出Catalan数的计数公式。

（九）容斥原理和鸽巢原理

1,掌握容斥原理的基本公式并利用基本公式解决一些应用问题。
2,掌握利用容斥原理基本公式解错排问题的方法。
3,掌握利用棋盘多项式的概念解决一些有限制的排列问题。
4.掌握二项式反演和Mobius反演的基本方法,解决一些问题。
5.掌握鸽巢原理的几种表述方法,并用鸽巢原理解决一些问题。注意将鸽巢原理与一些别的数学概念及技巧结合起来应用的方法。
6.掌握分析一些典型的Ramsey问题的方法。
7,掌握推算一些简单的Ramsey数的方法。

(十) Polya定理

1·掌握群的基本概念和定理。
2.掌握置换群的基本概念。
3,掌握置换的轮换、对换等表示方法和奇偶置换的概念。掌握正多面体的计算方法和转动群的分析方法。
4,掌握含不动点的置换子群、置换群作用下对象的轨道(等价类)等概念。掌握推导Burnside引理、Polya定理的方法。利用Burnside 引理和Polya定理解决一些应用问题。
5.掌握母函数型Polya定理的推导和应用。6,利用Polya定理解决图的计数问题。

三、思考题

说明:以下按照考试大纲与复习指南的十大部分,每一部分分别给出思考题和选择题。
(一）命题逻辑的等值演算和推理演算
1,什么是命题?什么是真值、真命题、假命题?
2.什么是命题联结词?它们的主要性质有哪些?
3.什么是合式公式?什么是重言式、矛盾式和可满足式?
4,如何判断两个命题公式是否等值?
5,如果仅仅知道命题公式的真值表,是否可以构造命题公式本身?应该如何构造?
6,n个命题变项可以构造多少个彼此独立的真值函项?

7,下列语句中( )是命题,并判断是简单命题还是复合命题。
(B) 吃饭了吗?
(A)好大的一场雪!
(C)如果天不下雨,我就骑车去。
(D)我正在说谎。

8,下列联结词不满足交换律的是( )。
(A) →
(B) ∧
(C) ∨
(D) ↔

9,下列合式公式中,( )不是重言式。
(A) Q→(P∨Q)
(B) (P∧Q)→P
(C) ¬ (P∧┐Q)∧(¬ P∨Q)
(D) (¬P∨Q)↔(P→Q)

10,给定命题公式(PVQ)-R,该公式在联结词的完备集 {¬,→} 中的形式为( ),在 {¬,∧} 中的形式为( ),在 {¬,∨} 中的形式为( )。

11,命题公式¬(P→Q)的主析取范式为( ),主合取范式为( )。

12,给定前提 →(P∧→Q), →Q∨R, →R, 则逻辑推论为( )。

13,命题逻辑的公理系统可简述为( )。
(A)用来建立公理的系统
(B)用公理产生推理规则的系统
(C)用来完善已有公理的系统
(D)从精选的几条公理出发,根据规定的演绎规则,推导出一系列定理的形式符号系统

14,通常一个公理系统包括以下哪几个部分( )。
(A)初始符号
(B)形成规则
(C)公理
(D)变形规则
(E)建立定理
(F)以上所有部分

(二)谓词逻辑的等值演算和推理演算
1,谓词逻辑与命题逻辑有哪些主要区别?它应提供哪些命题逻辑中不具备的功能,又可能带来哪些复杂的新问题?
2,谓词逻辑的公式应如何分类?判断任一公式的普遍有效性是否存在可行的方法?
3,在谓词逻辑中等值是如何定义的?谓词逻辑有哪些与命题逻辑类似的等值公式,如何证明它们的正确性?
4,任一谓词公式是否可化为与之等值的范式?这种范式形式是否唯一？
5,如何使用范式来简化对任一公式的普遍有效性与不可满足性的判定？
6,在谓词逻辑中如何进行推理演算?如何处理谓词逻辑中出现的量词？
7,归结法是否也适用于谓词逻辑?如何使用归结法进行谓词推理公式的证明?
8,设论域S={a,b,c} ,消去公式(∀x)P(x) ∧(∃x)Q(x)中的量词后,公式可化为( )。

9,将下列语句形式化:
(1)并非每个实数都是有理数[R(x):x是实数,Q(x):x是有理数]。
(2)没有不犯错误的人[P(x) :x是人,F(x) :x犯错误]。
(3)尽管有人聪明,但未必一切人都聪明[P(x) :x是人,C(x) :x聪明]。

10,下面的等值式中不正确的是( )。(其中Q是命题变项,与个体变元x无关。)
(A) (∀x) (P(x) ∨Q)=(∀x)P(x)∨Q
(B) (∃x) (P(x) ∨Q)=(∃x)P(x)∨Q
(C) (∀x) (P(x)→Q) =(∃x)P(x)→Q
(D) (∃x) (P(x)→Q)=(∃x) P(x)→Q

11,使用归结法证明(∀x) (P(x) ∨Q(x)) ∧ (∀x) (Q(x)→¬R(x)) ∧ (∀x)R(x) =>(∀x)P(x)。

(三）集合与关系
1,在集合运算中是否满足类似命题逻辑中的摩根律?
2,自然数在集合论中应如何表示?0又是如何表示的?
3.集合与二元关系存在哪些共同点?一个具有n个元素的集合可以定义多少个二元关系?
4,二元关系具有哪些主要性质?这些性质应如何定义和判断?
5.怎样对一个已知关系增加一些原来不具有的特殊性质,从而构成一个新的关系?
6,一个二元关系是等价关系的条件是什么?是偏序关系的条件又是什么?
7.一个关系应满足哪些条件才成为函数?任意集合上的函数应如何定义?
8.从集合A到集合B不同的函数共有多少个?如何构造从集合A到B的一对一且A到B上的函数(双射)?
9.一个无限集合的无穷子集是否与原集合的基数相同?实数集的基数是否与自然数集的基数相同?
10.什么是连续统假设?

11,对任意的集合A、B和C,判断下列命题是否为真。
(1)若A∈B且B⊆C,则A∈C
(2)若A∈B且B⊆C,则A⊆C
(3)若A⊆B且B∈C,则A∈C
(4)若A∈B且B⊄C,则A∉C

12.选择正确的答案填入到括号中。设s={∅, {1}, {1,2}},则有
(1)( )∈S (A) {1,2}(B) 1 (2)( )⊆S (A) {{1,2}} (B) {1} (3)P(S)有( )个元素 (A) 3 (B) 6 (C)7 (D) 8 (4)|S|=( ) (A) 3 (B) 6 (C)7 (D) 8 (5)( )既是S的元素,又是S的子集 (A) {1} (B)∅

13,设R={a,b,c},S={1,2},从R到S不同的二元关系共有( )个。
(А) 6 (B)7 (C) 32(D) 64

14,设集合A={1,2,3,4}上的二元关系,R={<1,1>,<2,3>,<2,4>,<3,4>},则R具有( )。
(A)自反性 (B)传递性 (C)对称性 (D)非自反性

15,设集合A={1,2,3,4}上的二元关系
R={<1,1>,<2,2>,<2,3,<4,4>},
S={<1,1>,<2,2>,<2,3,<3,2>,<4,4>}
则S是R的( )闭包。
(A)自反 (B)传递 (C)对称 (D)以上都不对

16,设集合A={a,b}上的二元关系R={<a, a>, <b, b>},则R( ）。
(A)是等价关系但不是偏序关系
(B)是偏序关系但不是等价关系
(C)既是等价关系又是偏序关系
(D)既不是等价关系也不是偏序关系

17,设A={a,b,c,d},B={1,2,3 },从A到B不同的函数共有( )个。
(A) 12 (B)64 (C)81 (D) 1024

18,设R为实数集,函数f:R-R,f(a) =-a²+2a-1,则f是( )。
(A)单射而非满射 (B)满射而非单射
(C)双射 (D)既不是单射也不是满射

19,对任意的无限基数k,选择合适的关系符: χ₀( )k。
(A) < (B) ≤ (C)= (D)≥ (E) = (F)以上都不对

20,连续统假设的主要内容是:断言x.<k<i,成立的基数k( )。
(A)肯定不存在
(B)猜想存在,但数值待定
(C)猜想这样的不存在,但尚未证明
(D)k已找到

(四）图论的基本概念、道路与回路
1,图的定义是什么?
2,图G中V₂、V₄的出度、入度及度各为多少?
3,简单图G中,若m>½(n-1)(n-2),证明G中不存在孤立顶点。
4,证明在有向完全图(竞赛图)中

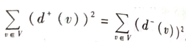
5.写出图G的邻接矩阵与关联矩阵。

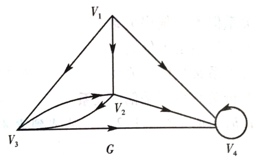
6.什么是有向途径(链)?有向路与有向迹?它们有什么区别?
17.欧拉环游(欧拉回路)与汉密尔顿回路的区别是什么?
8·证明若连通图G有不同的最长路,则它们必定相交。
9,设G是n 3的简单图,若m(n-1)(n-2)+2,证明G中存在汉密尔顿回路。
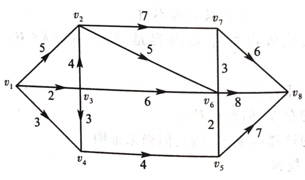
10.求下图中v₁到各点的最短路。

(五)树、平面图与图的着色
1,树连通吗?有回路吗?树中任意两点间可否有多条不同的路?
2,若树中度为2的点有n₂个,度为3的点有n₃,个, ,度为k的点
有nk个。试问有多少个点的度为1?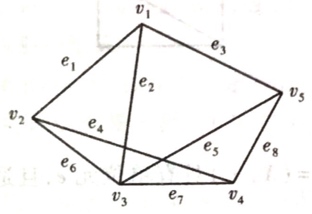

3.求F图G中
(1)支撑树的数目。
(2)必含(V₂,V₃)的支撑树数目。
(3)不含(V₂,V₃)的支撑树数目。

4.图的块一定是完全图吗?说明理由。
5,设图G的赋权矩阵是

求它的最短支撑树。

6.证明平面图的欧拉公式是n-m+f=2,其中n、m和f分别表示图G的顶点个数、边数和面数。试问简单平面图中至少有一个顶点的度小于几?

7,证明在n≥4的极大平面图中,每个顶点的度都大于等于3。

8,设G是无割边的平面图,且每两个域(也称“面”)之间最多有一条公共边,证明
(1)G中至少有两个域有相同的边界数。
(2)若各域的最小边界数是5,则G中最少有12个域。
(3)求下图的色数和色多项式。

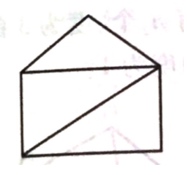
(六)代数结构
1.设代数系统V=(x, · )具有单位元e,且适合结合律,若a,b∈X且可逆, 证明a·b也是可逆的,并且(a·b)⁻¹ = b⁻¹ * a⁻¹ 。
2.设K={e,a,b,c} ,定义二元运算·如下:

试问(K, ·)是否是可结合的?有无单位元?每一个单位元是否可逆?

3.设(s, ·)是半群,且左右消去律都成立,证明S是交换半群的充要条件是对任意a,b∈S有:(ab)² =a²b²

4.已知代数系统(S, *)和(P, ·),其中S={a,b,c}, P={1,2,3}。二元运算分别定义为:

试证明它们是同构的。

5,群、环、域的定义有什么区别?

8,说明Klein四元群是否为循环群。

9,试证明Sn中的每个元都可以表示成(12), (13), ···,(1n) 这n-1个对换中若干个的乘积形式。

10,设G是阶为6的群,证明G中一定有且只有一个3阶子群。

11,设H₁、H₂、H是G的正规子群,且H₁⊂H₂, 证明H₁H是H₂H的正规子群。

12.设f是G₁到G₂的同态,g是G₂到G₃的同态, 证明gf是G₁到G₃的同态,且gf的核是f⁻¹g⁻¹(e”) ,其中e”是G₃的单位元。

(七) 排列与组合
1.什么是加法法则与乘法法则?
2.1-1 000的整数中共出现了多少个0? 3.6个人分乘2辆4座轿车(座位有区别)有( )种方案。
(A) 720(B) 120(C) 40320 (D) 10800

4.10个男生和5个女生围成一圈,女生两两不相邻,有( )种方案。
(A) 10!5! (B) (10+5)!
(C) 9!10·9·8·7·6 (D) 10·11·12·13·14

5.6个相同的球放入4个不同的盒子里,有多少种方案?

6.红、蓝、橙、黄、绿色珠子各一颗,串成一串项链,有多少种方案?

7.展开(x+y+z)⁴ 。

8.v₁、v₂、v₃、v₄ 这四个顶点构成一棵树,有多少种方案?

9,红、黄、蓝、绿四种颜色的旗帜各四面,这16面旗帜排成一列问有多少种不同的排列方法?

10.能除尽600的正整数的数目是多少?

11.证明

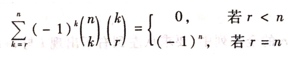
其中rn是正整数。

(八)母函数与递推关系
1,求n位二进制数中相邻两位不出现11的数的个数。
2,满足上题要求的所有n位二进制数中一共出现了多少个1?

3,用红、蓝、白三色珠子n颗穿成一串,要求红色珠子在串中出现偶数个(2,4,···),设满足要求的穿成n颗一串的方案数为Cn。
(1)求序列{Cn}的指数型母函数。
(2)计算Cn的值。

4,设x+2y+32=n的非负整数解(x,y,z)的组数为En,求:
(1)En的普通型母函数。
(2)En的通项公式。

5,在同一平面上画一个圆和n条直线,每条直线均与其他直线在圆内相交。若没有三线及以上共点的情形,则这些直线将圆的内部分成多少块区域?

6.求1³+2³+···+n³，n是整数。

7,在由a、b、c、d、e构成的n位字符串中,不允许出现一个字符连续出现3次的情况,这样的n位串有多少个?

8,在上题中,在所有符合要求的串中,一个字符连续出现2次的情况一共有多少次?

9,一个平面上的n条直线无平行及3线共点的情况,一共把平面分成多少个不重叠的域?

10,n个平面中无平行、3平面共线及4平面共点的情况,一共把空间分成多少个不重叠的域?

(九)容斥原理及鸽巢原理
1,证明n元集合N到m元集合M(n≥m)的满射的个数为

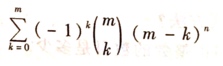
2.n对(n≥2)夫妇围圆桌而坐,要求每对夫妇不相邻,有多少种方案?

3,在1~n的全排列中,要求从左到右不出现i与i+1 (i=1,2,···,n-1)相邻,这样的排列有多少?

4,在1~n构成的圆排列中,顺时针扫描,要求不出现i与i+1 (i=1 ,···,n-1)相邻及n与1相邻的情况,这样的圆排列有多少?

5,求下列集合中不是n²、n³形式的数的数目,n是正整数: { 1,2,···,10⁴}

6,求下列集合中不是n²、n³形式的数的数目: {10³, 10³+1,···,10⁴}

7,求证:用2种颜色给完全图k₆的边进行着色,则一定存在两个单色三角形。

8,证明2维欧氏空间中:
(1)5个整点中必有2个整点的重心是整点。
(2)9个整点中必有3个整点的重心是整点。
这里: (xi , yi)(i=1,···,n)的重心是指

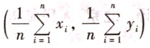
9.17个学生两两之间打乒乓、网球或羽毛球,证明必有3个学生相互之间打同一种球。

10,随意地把一个3x9棋盘的每个方格涂成红色或蓝色,求证:必有两列方格,它们的涂色方法是一样的。

(十) Polya 定理
1,写出对称群S₅,每种置换格式的个数。

2,写出与S₅,对应的以5个顶点完全图的边为目标集的置换群的不同格式的置换的个数。

3.G是有限群,x是G的元素,则 的阶必除尽G的阶。

4,设v₁、v₂、v₃是圆周上3等分点,要在v₁、v₂、v₃每点处镶上一个珠子。用红、蓝、绿3种颜色的珠子镶上,试问有多少种不同的方案?

5,在正六面体的每个面上任意作一条对角线,有多少种方案?

6,对正四面体的顶点3着色、棱2着色、面4着色有多少种方案?

7,正六面体的6个面分别用红、蓝两种颜色着色,问有多少种不同的方案?

8、将一个立方体的8个顶点中的5个涂红色,其余3个涂蓝色,试问有多少种涂色方案?

四、参考书目

[1]石纯一,王家廊,数理逻辑与集合论. 2版.北京:清华大学出版社, 2000. [2]王宏,杨明,数理逻辑与集合论.精要与题解.北京:清华大学出版,2001.
[3]耿素云,屈婉玲.离散数学.北京:高等教育出版社,1998. [4]卢开澄,卢华明,组合数学.4版.北京:清华大学出版社,2006
[5]王树禾.图论.北京:科学出版社,2004.
[6]Gary Charttrand, Ping Zhang.图论导引,范益政,汪毅,龚世才,等译.北京:人民邮电出版社,2007.