MyWiki知识管理

组合数学-常系数递推关系

母函数解递推关系(递推方程) - 要点总结

我们有一个序列，要求它的通项公式。我就把它设一个辅助函数叫母函数，我只要把母函数找出来把它分解开，x的n次方的系数，就是我要求的那个序列H(n)的通项表达式了。

求母函数两种可能性：
第一个：这个母函数根据实际意义可以写出来。比如之前例子中的摇骰子，或者那种r个球放入n个不同盒子里，那可以根据实际意义直接写出来的，然后你把它展开；
第二种是有递推关系的。可用迭代的方法解决，但这个方法很麻烦，有个更简单的办法就是把递推化成特征方程，求特征根，有了特征根之后解出递推关系的一般解，然后把它的系数根据初始条件求出来，得到一般通项式。

根据递归关系得到特征方程

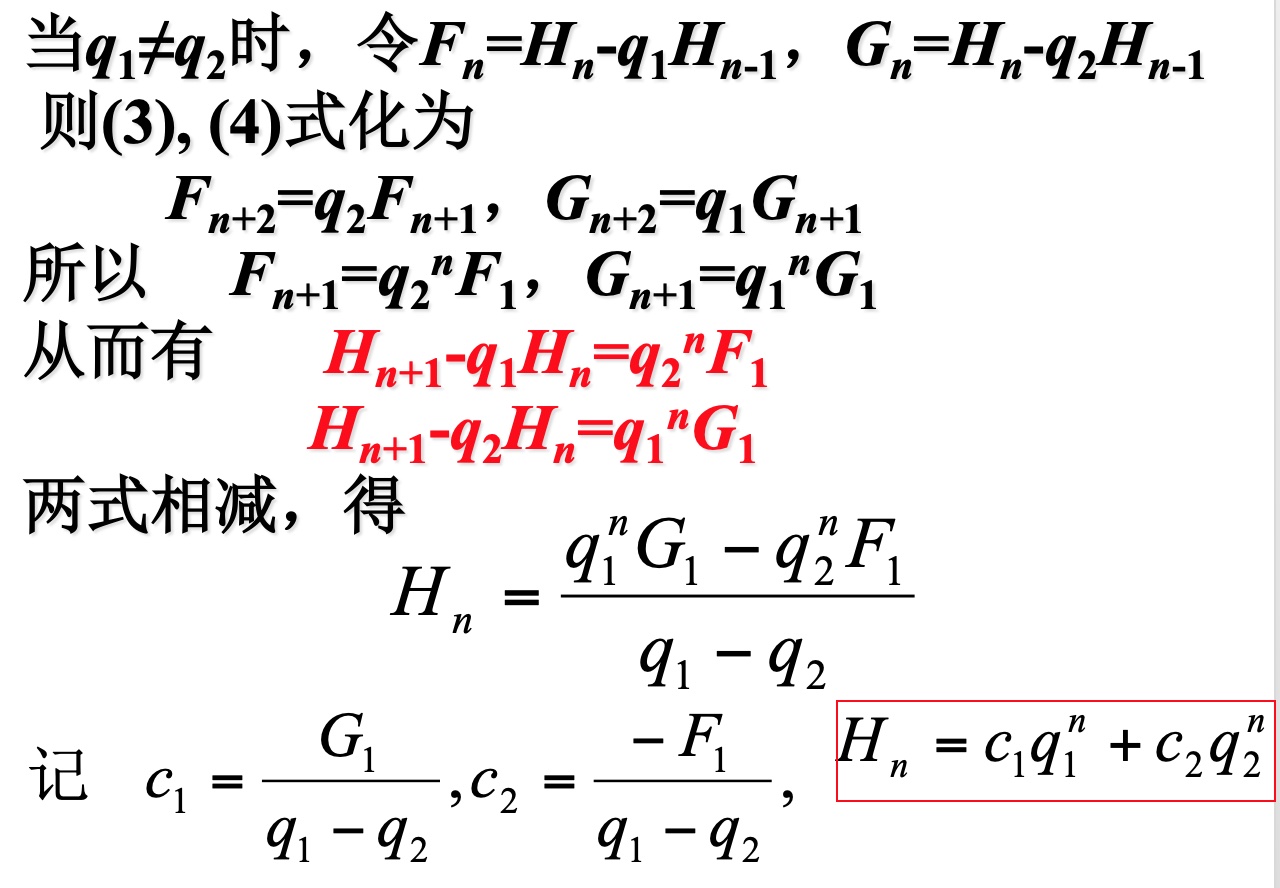
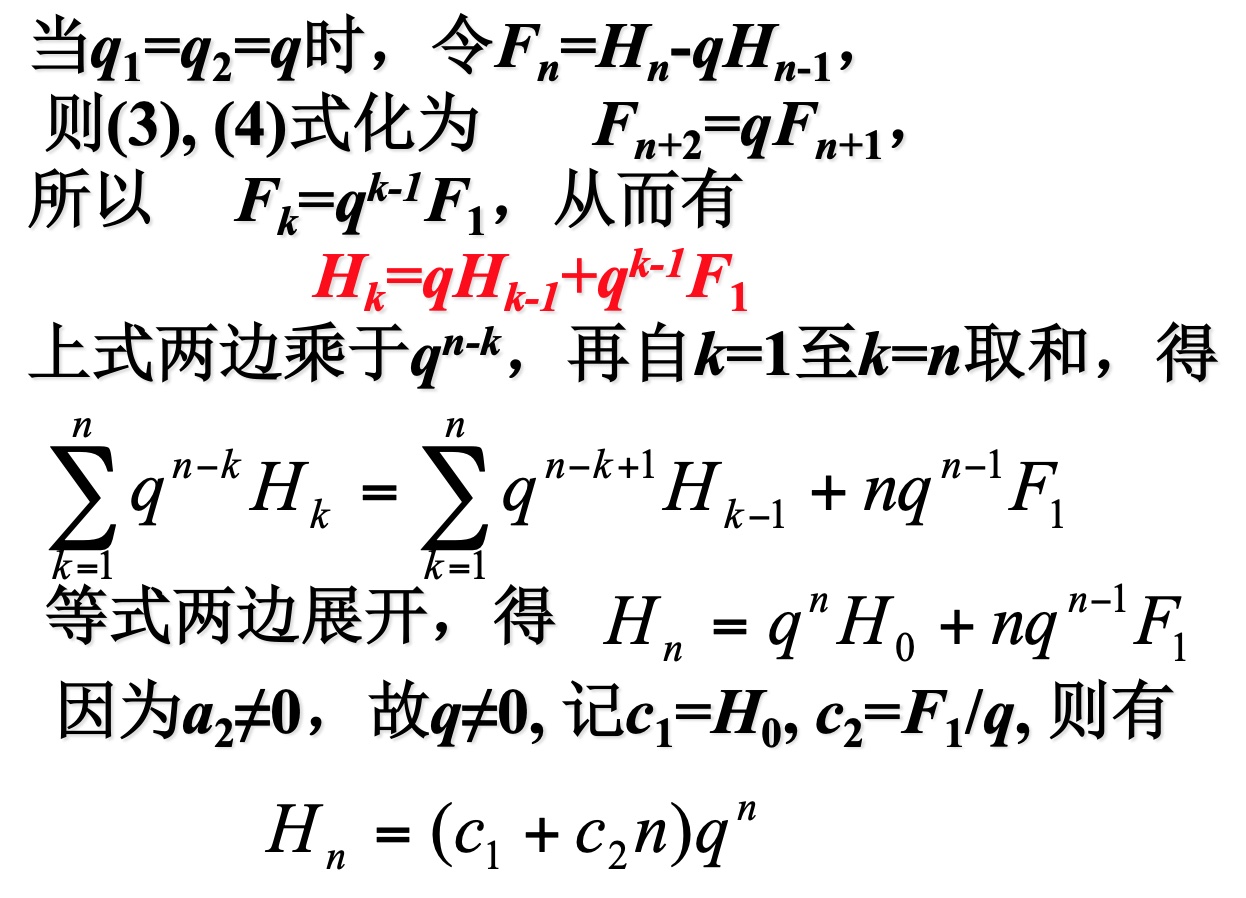
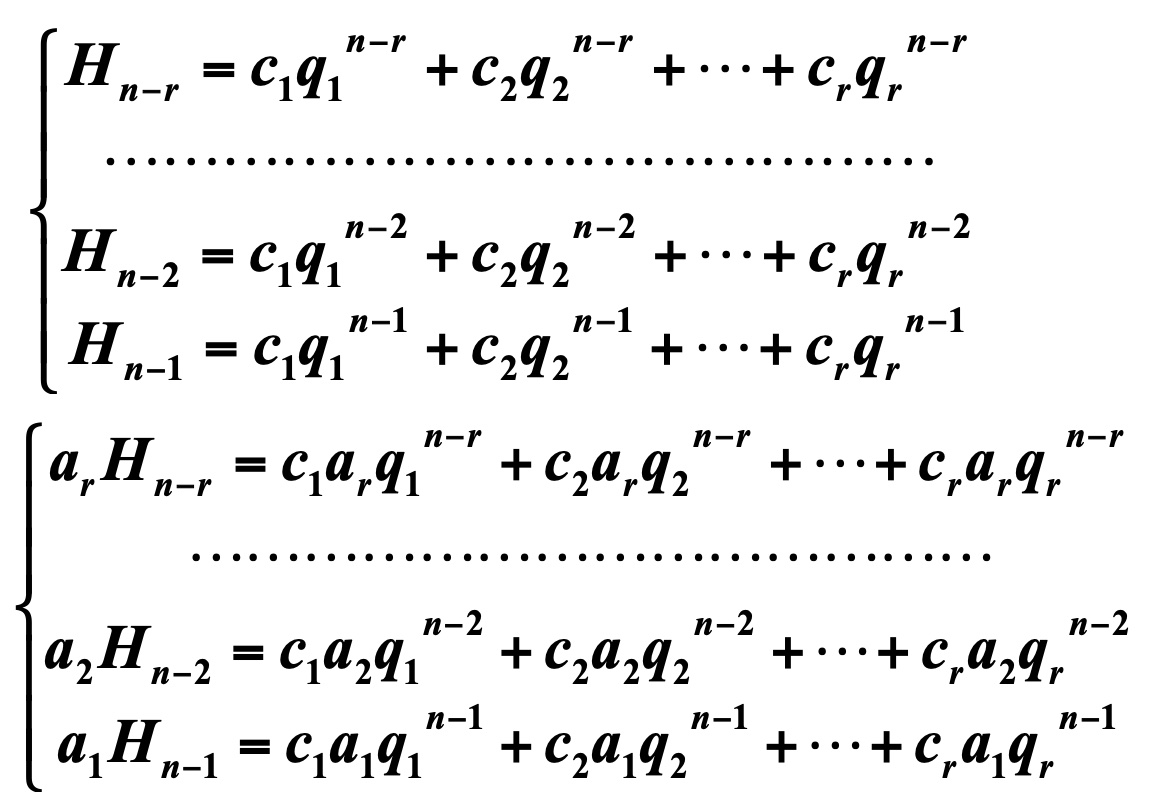
$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

$根据递归关系得到特征方程$

使用递推方程求解Fibonaccio数列的通项公式

$根据递归关系得到特征方程$
$根据递归关系得到特征方程$
$根据递归关系得到特征方程$
$根据递归关系得到特征方程$
$根据递归关系得到特征方程$
$根据递归关系得到特征方程$
$根据递归关系得到特征方程$

特征根有重根的情况

$特征根有重根的情况$
$特征根有重根的情况$ $特征根有重根的情况$

仅有两个有复特征根

$特征根有重根的情况$
$特征根有重根的情况$
$特征根有重根的情况$
$特征根有重根的情况$
$特征根有重根的情况$
$特征根有重根的情况$
$特征根有重根的情况$
$特征根有重根的情况$
$特征根有重根的情况$

常系数线性非齐次递归关系

$常系数线性非齐次递归关系$
$常系数线性非齐次递归关系$
$常系数线性非齐次递归关系$
$常系数线性非齐次递归关系$
$常系数线性非齐次递归关系$
$常系数线性非齐次递归关系$
$常系数线性非齐次递归关系$
$常系数线性非齐次递归关系$
$常系数线性非齐次递归关系$

版权所有，转载请注明出处 luowei.github.io.