组合数学-排列组合
组合数学的很多问题:关键是找到一一对应,把问题转化成容易理解和解决的。
可重排列
可重排列的两种理解方式:
- 先认为这N个东西都是不一样的,有N!排列方式。但实际上呢,这N1个a1是一样的,所以要把重复的给除掉,除以N1!;同样N2个a2我们原来也以为他们是不一样的,但实际上他们是一样的,所以同样还要除以N2!,其他的也一样要除掉,除完。
- 我一共就N个位置,要把这些所有东西放进去。我先从这N个里头挑出N1个位置出来,然后就把这N1个a1放进去,把这N个位置当中的N1个位置放完;我在从里头挑N2个位置出来,把那N2个a2放进去;再从剩下的N-N1-N2里挑N3个位置所a3放进去;到最后放ak的时候,就只剩下Nk个位置放Nk个东西了;然后再把所有的表达式代入化简,即得。



可重组合
做组合有点像把那个小学奥数一样,他没有多少预备知识,他考的是你会不会换一个角度看这个问题。换一个角度看这个问题,就是你有没有好的方式把他对应到一个好算的东西上去。其关键还是一个找一一对应的问题。
可重组合的解决思路:
问题:现在问题是从N个不同的数里挑出r个数出来,允许重复挑,有多少种挑法。
- 方法一
思路:我把它反过来看成是把r个相同的球放入N个不同的盒子,盒子编号从1到N,然后我就把这r个球往这些盒子里放。比如1号盒子放几个球就相当于我取了几个1,2号盒子放几个球就相当于我取了几个2,放完之后,哪个盒子里有几个球就相当于我从这个盒子里取了几个相同的数。所以1到N个数里取r个数做可重复的组合,与把r个相同的球往N个不同的盒子里放是一一对应的。 即问题转化成了:把r个相同的球放入N个不同的盒子有多少种放法。
再作转换:N盒子我可把它看成是在一个大容器中有N-1块相同的隔板分隔出了N个不同的盒子,隔板是可以移动的。所以r个球往N个盒子里放,就相当于n-1个隔板与r个球的排列,即(N-1+r)!/(r!·(N-1)!) 种放法。两次找一一对应。
- 方法二
使用代数的方式,如下图演算。



不相邻组合



组合恒等式
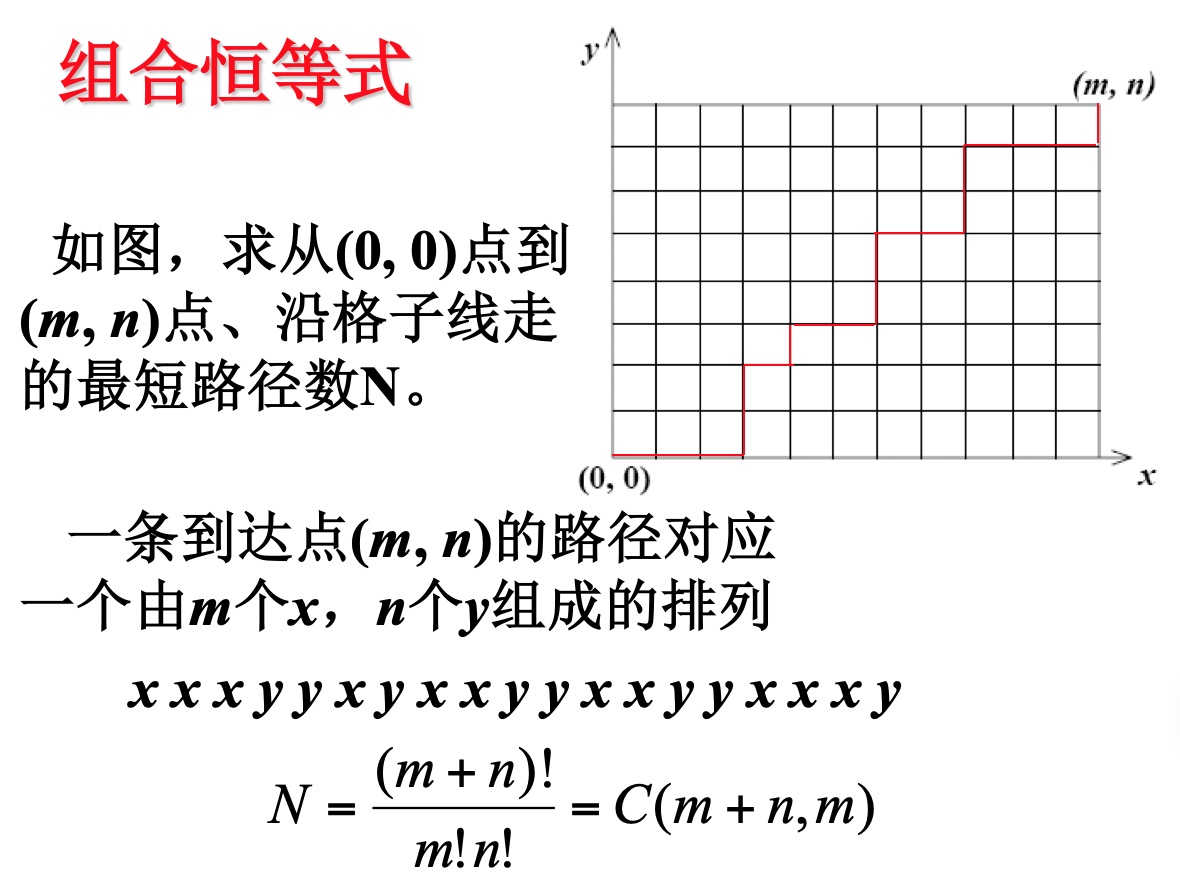

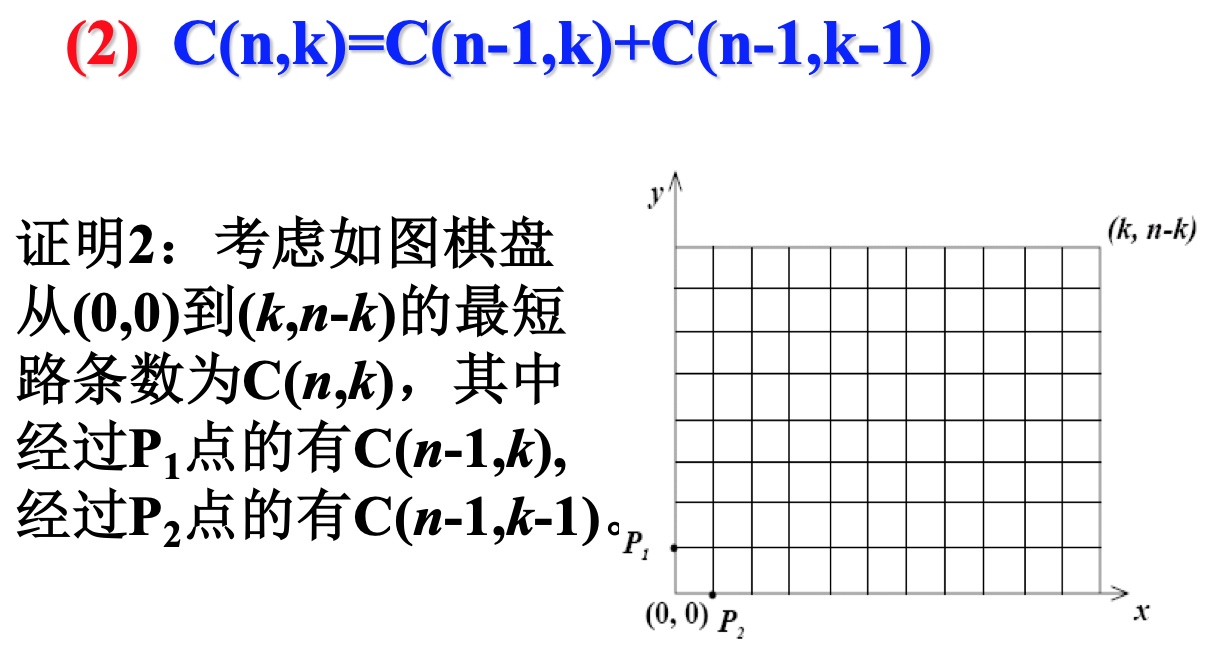



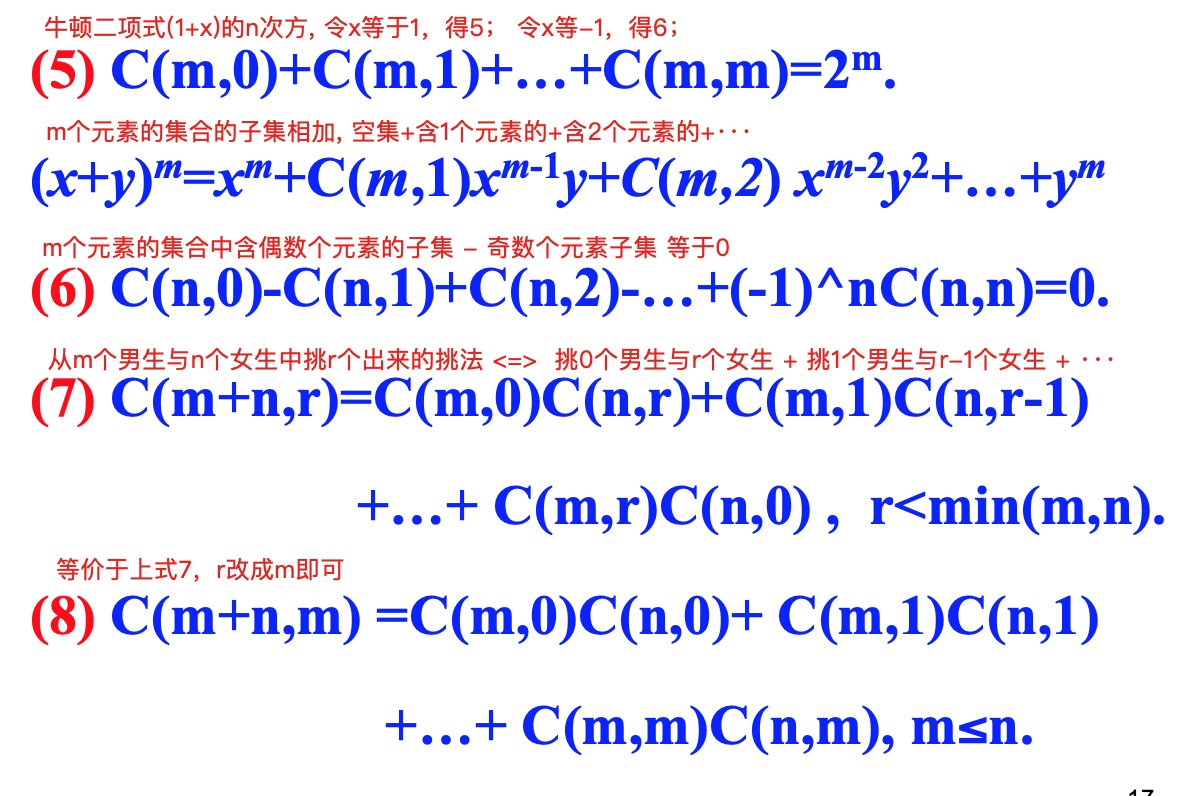
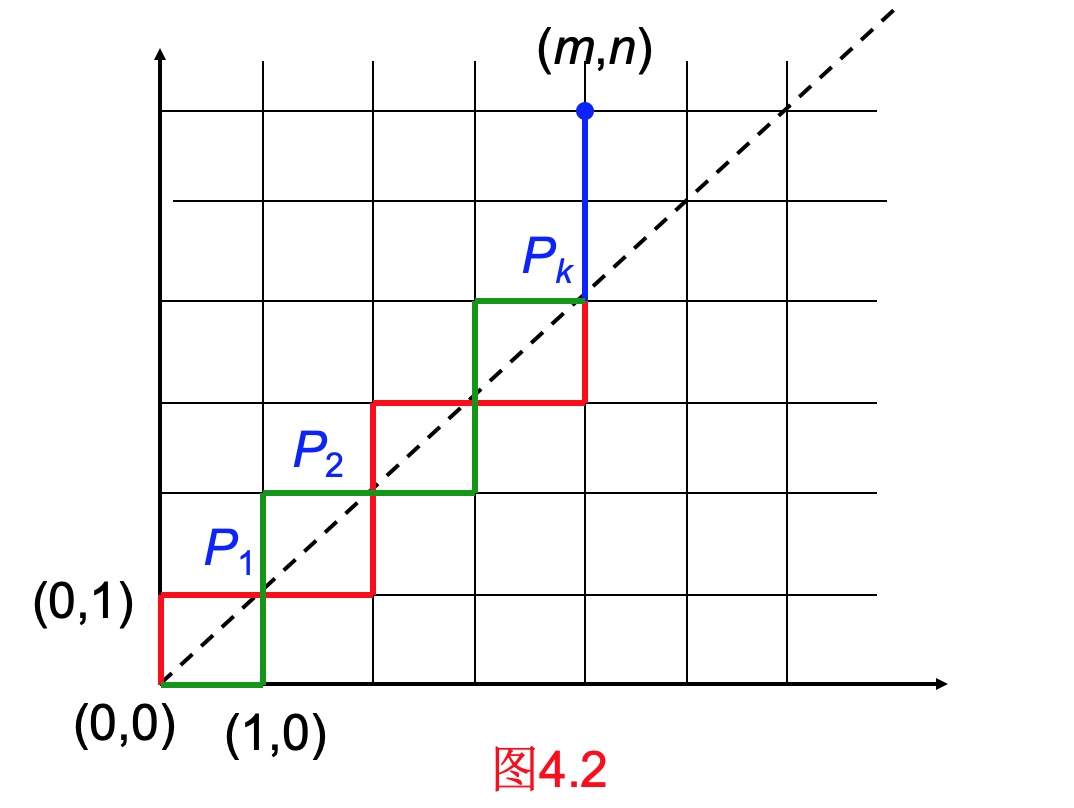
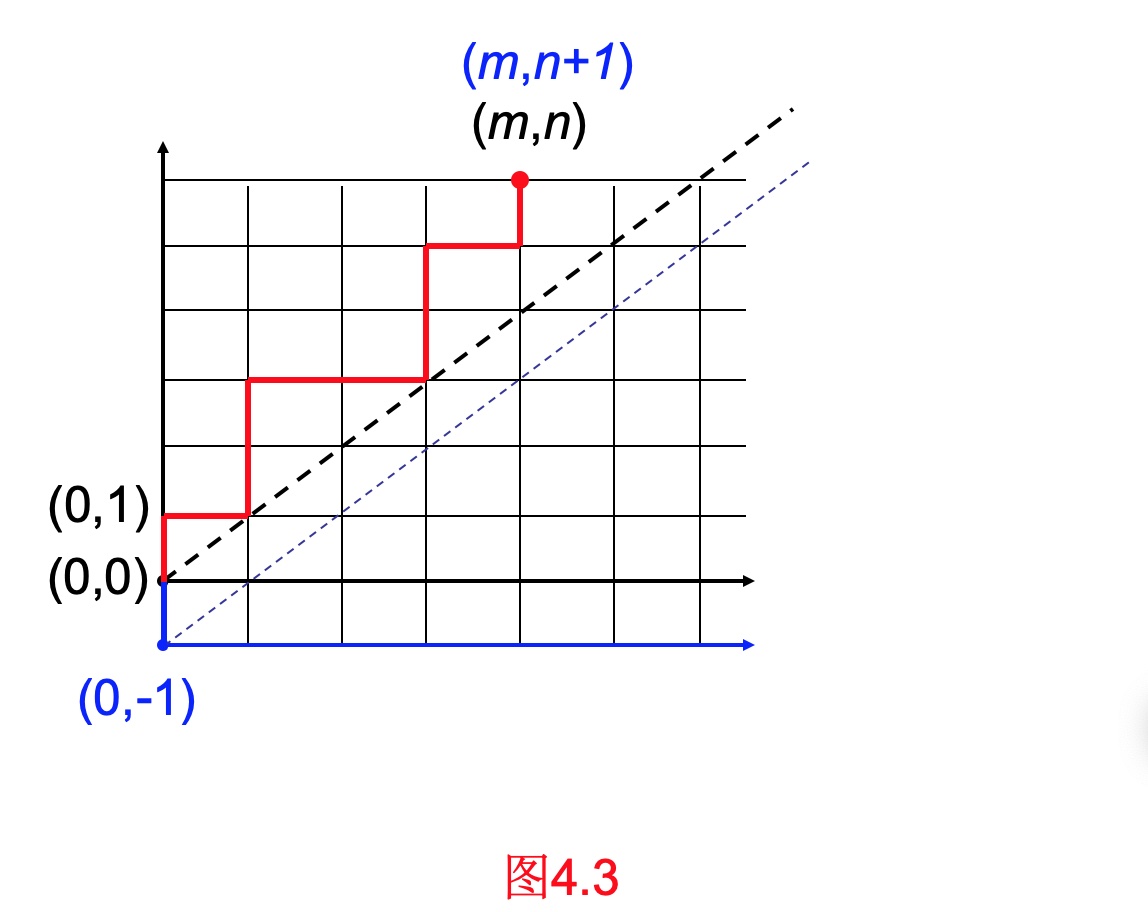
与路径有关的问题

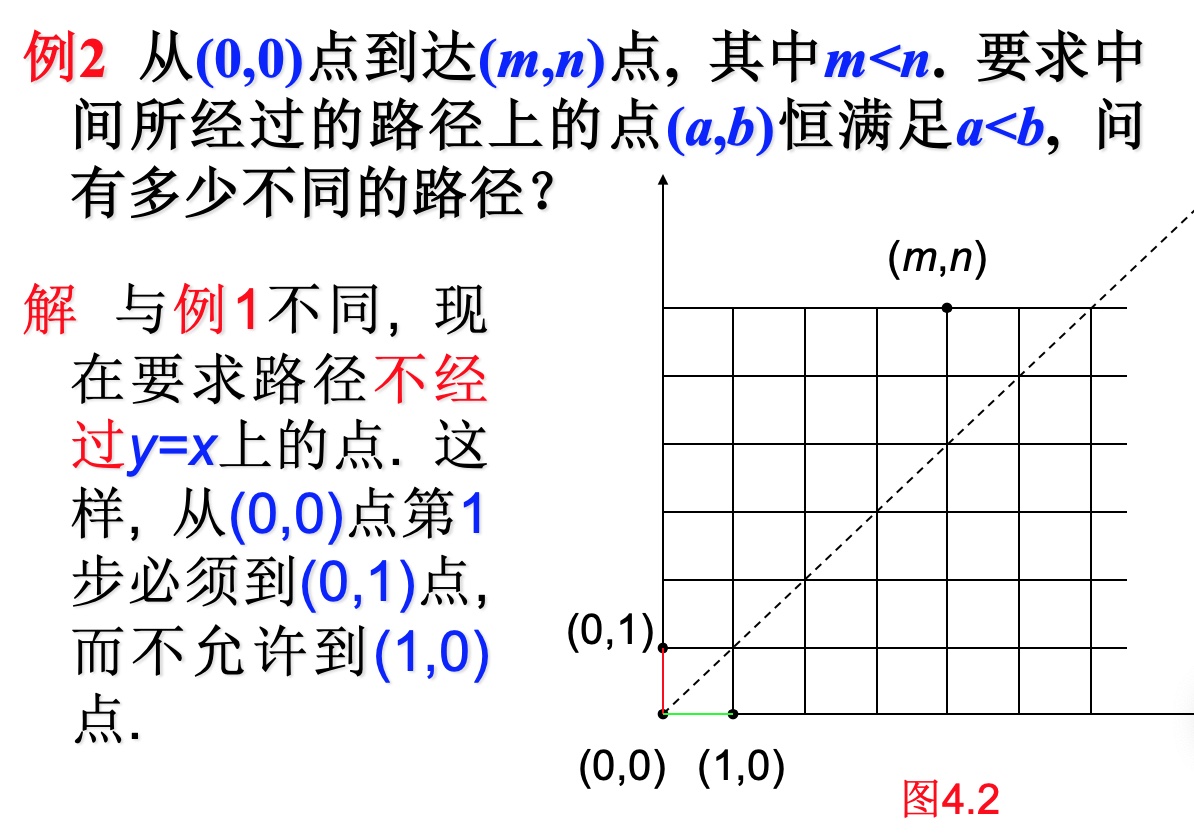










Stirling近似公式


例子

