数据结构-串、树、二叉树、查找二叉树及图
串
str.h
//str.h
#ifndef _STR_H
#define _STR_H
typedef struct
{
char *ch;
int len;
}STR;
STR *NewStr(char *str);
void DestroyStr(STR *s);
void ClearStr(STR* s);
int StrCompare(STR *s,STR *t);
int StrCancat(STR *s,STR *t);
STR *SubStr(STR *s,int pos,int len);
#endif
str.c
//str.c
#include<stdio.h>
#include<stdlib.h>
#include "str.h"
STR *NewStr(char *str) //新建一个串
{
STR *s=NULL;
int i;
s=(STR *)malloc(sizeof(STR));
if(s==NULL)
return NULL;
for(i=0;str[i];++i);
s->ch=(char *)malloc((i+1)*sizeof(char));
if(s->ch==NULL)
{
free(s);
return NULL;
}
s->len=i;
while(i>=0)
{
s->ch[i]=str[i];
--i;
}
return s;
}
void DestroyStr(STR *s) //销毁串
{
free(s->ch);
s->ch=NULL;
s->len=0;
}
void ClearStr(STR* s)
{
free(s->ch);
s->ch=NULL;
s->len=0;
}
int StrCompare(STR *s,STR *t)//比较串
{
int i;
for(i=0;i<s->len && i<t->len;i++)
if(s->ch[i]!=t->ch[i])
return s->ch[i]-t->ch[i];
return s->len-t->len;
}
int StrCancat(STR *s,STR *t)//连接两个串
{
int i;
char *temp=NULL;
temp=(char *)malloc((s->len+t->len+1)*sizeof(char));
if(temp==NULL) return 0;
for(i=0;i<s->len;i++)
temp[i]=s->ch[i];
for(;i<s->len+t->len;i++)
temp[i]=t->ch[i-s->len];
temp[i]=0; //在最后加上'\0'
ClearStr(s);
s->ch=temp;
s->len=i;
return 1;
}
STR *SubStr(STR *s,int pos,int len) //获取子串
{
STR *t=NULL;
if(pos<1||pos>s->len||len<0||len>s->len-pos+1)
return NULL;
t=NewStr("");
ClearStr(t);
t->ch=(char *)malloc((len+1)*sizeof(char));
if(t->ch==NULL) return NULL;
t->len=len;
for(--len;len>=0;--len)
t->ch[len]=s->ch[pos-1+len];
t->ch[t->len]=0;
return t;
}
main.c
//main.c
#include<stdio.h>
#include<stdlib.h>
#include "str.h"
void main()
{
int res;
STR *t=NULL,*s=NewStr("hello");
printf("s=%s,len=%d\n",s->ch,s->len);
t=NewStr("hello");
res=StrCompare(s,t);
if(res==0)
printf("s=t\n");
else if(res>0)
printf("s>t\n");
else
printf("s<t\n");
ClearStr(t);
t=NewStr("world");
StrCancat(s,t);
printf("s=%s,len=%d\n",s->ch,s->len);
DestroyStr(t);
t=SubStr(s,2,5);
printf("t=%s,len=%d\n",t->ch,t->len);
DestroyStr(s);
}
树
tree.h
//tree.h
#ifndef _TREE_H
#define _TREE_H
typedef struct _node //定义树的结点
{
void *data;
struct _node *parent;
struct _node *child;
struct _node *next;
}TREE;
int InsertTree(TREE **t,void *data,int size);
int DeleteAllTree(TREE *t);
int DeleteTree(TREE *t);
TREE *GetTreeByKey(TREE *r,void *key,int(*compare)(void*,void *data));
int PrintTree(TREE *t,void(*print)(void *));
#endif
tree.c
//tree.c
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include "tree.h"
int InsertTree(TREE **t,void *data,int size)
//第1个参数为目录指针变量的地址,第2个参数数据无类型,第3个参数数据的大小
{
TREE *p=(TREE *)malloc(sizeof(TREE));
if(p==NULL) return 0;
memset(p,0,sizeof(TREE));
p->data=malloc(size);
if(p->data==NULL)
{
free(p);
return 0;
}
memcpy(p->data,data,size);
//以上是创建一个新的结点
//--------------------------------
//以下是把数据存到新结点中去
if(*t==NULL) //如果目录结点为空
*t=p;
else if((*t)->child==NULL)//如果树中只有根结点
{
p->parent=*t;
(*t)->child=p;
}
else
{
TREE *tmp=(*t)->child;
while(tmp->next) //循环到这一层的最后一个结点
tmp=tmp->next;
tmp->next=p;
p->parent=*t;
}
return 1;
}
int DeleteAllTree(TREE *t) //删除整棵树
{
TREE *p=NULL;
while(t)//当树不为空时,往下做,直到树为空
{
if(t->child!=NULL)//如果子结点不为空
{
p=t->child->child;
while(p->next)//这个循环使p指向t的孙子结点下的最后一个
p=p->next;
//此时p已指向t的孙子结点下的最后一个
p->next=t->child->next;//将此时p的下一个指向t的子结点的下一个(即t的最右子结点)
t->child->next=NULL;//将指向t子结点的兄弟结点清空
}
p=t->child;//将t的子结点赋给p指针,以记录t的子结点
free(t->data);
free(t);
t=p; //将p重新赋给t指针
}
return 1;
}
int DeleteTree(TREE *t)//删除一个树结点
{
if(t==NULL) return 0;
if(t->parent==NULL) //如果t为根结点
;
else if(t==t->parent->child)//如果t是某一层的第一个结点
t->parent->child=t->next;//将t的下一个挂到t的位置
else
{
TREE *p=t->parent->child;//将t结点所在的这一层的第1个兄弟结点赋给p
while(p->next==t)//p往下找,直到找到p的下一个是t结点,即找到t的上一个
p=p->next;
p->next=t->next;//把p的上一个的next指针指向t的下一个,这样就从树中删除了t结点
}
DeleteAllTree(t);
return 1;
}
TREE *GetTreeByKey(TREE *r,void *key,int(*compare)(void*,void *data))//查找结点
{
if(r==NULL)
return NULL;
if(compare(r->data,key))
return r;
if(GetTreeByKey(r->child,key,compare))
return r->child;
if(GetTreeByKey(r->next,key,compare))
return r->next;
return NULL;
}
int PrintTree(TREE *t,void(*print)(void *))//打印树
{
int i=0;
TREE *p=t->child;
while(p)
{
print(p->data);
i++;
p=p->next;//让p指向它的兄弟
}
return i;
}
main.c
//main.c
//用树表示目录层次
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include "tree.h"
TREE *root=NULL,*curDir=NULL;//根目录、当前目录
void ParseMkdir(char *com)//创建目录
{
if(InsertTree(&curDir,&com[6]/*从Mkdir 后一个字符开始截取*/,strlen(&com[6])+1)==0)
{
printf("命令操作失败!\n");
}
}
int CompareDir(void *data,void *key)
{
return strcmp((char*)data,(char *)key)==0?1:0;
}
void ParseRmdir(char *com)//删除目录
{
TREE *p=GetTreeByKey(root,&com[6],CompareDir);
if(p==NULL)
printf("文件不存在!");
DeleteTree(p);
}
void ParseCd(char *com)//切换目录
{
}
void PrintDir(void *data)//打印目录
{
printf("%10s",(char*)data);
}
void ParseLs(char *com)//查看目录
{
if(PrintTree(curDir,PrintDir)==0)
printf("没有目录!");
printf("\n");
}
void main()
{
char str[1024];
InsertTree(&root,"/",2);
curDir=root;
while(1)
{
printf("mkdir创建目录;\nrmdir删除目录;\nls查看目录;\ncd切换目录;\nexit退出\n");
printf(">>>:");
gets(str);
fflush(stdin);
if(strstr(str,"mkdir")==str)
ParseMkdir(str);
else if(strstr(str,"rmdir")==str)
ParseRmdir(str);
else if(strstr(str,"cd")==str)
ParseCd(str);
else if(strstr(str,"ls")==str)
ParseLs(str);
else if(strstr(str,"exit")==str)
{
printf("bey!\n");
exit(0);
}
else
printf("command not find!\n");
}
}
二叉树
tree.h
//tree.h
#ifndef _TREE_H
#define _TREE_H
typedef struct node
{
char data;
struct node *lchild,*rchild;
}TREE;
TREE *MakeTree();
void PrintTreeByBefore(TREE *t);
#endif
tree.c
//tree.c
#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
#include "tree.h"
#include "stack.h"
TREE *MakeTree()
{
TREE *t=NULL;
char ch;
ch=getche();//读取字符并显示
if(ch=='#')
return NULL;
t=(TREE*)malloc(sizeof(TREE));
if(t==NULL) return NULL;
t->data=ch;
t->lchild=MakeTree();
t->rchild=MakeTree();
return t;
}
void PrintTreeByBefore(TREE *t) //先序打印
{
if(t==NULL)
return;
printf("[%c]",t->data);
PrintTreeByBefore(t->lchild);
PrintTreeByBefore(t->rchild);
}
void PrintTreeByMid(TREE *t)//中序方式
{
TREE *p=t;
STACK* s=InitStack();
Push(s,&t);//将根地址压到栈中
while(!IsEmpty(s))
{
while(p)
{
p=p->lchild;
Push(s,&p);//将p左结点压到栈中
}
Pop(s,&p);
if(!IsEmpty(s))
{
Pop(s,&p);
printf("[%c]",p->data);
p=p->rchild;
Push(s,&p);
}
}
DestroyStack(s);
}
void main()
{
TREE *tree=MakeTree();
PrintTreeByBefore(tree);
printf("\n*******************\n");
PrintTreeByMid(tree);
printf("\n");
}
stack.h
//stack.h
#ifndef _STACK_H
#define _STACK_H
#include "tree.h"
#define ElemType TREE*
#define STACK_INIT_SIZE 10
#define STACK_INCREME 10
typedef struct
{
ElemType *base;
ElemType *top;
int size;
}STACK;
STACK *InitStack();
void DestroyStack(STACK *s);
int Push(STACK *s,ElemType *e);
int Pop(STACK *s,ElemType *e);
int IsEmpty(STACK *s);
#endif
stack.c
//stack.c
#include<stdio.h>
#include<stdlib.h>
#include "stack.h"
STACK * InitStack() //初始化一个栈
{
STACK *s=(STACK*)malloc(sizeof(STACK));//初始化一个栈
if(s==NULL)
exit(0);
s->base=(ElemType*)malloc(STACK_INIT_SIZE*sizeof(ElemType));//为栈分配一个初始大小
if(s->base==NULL) //如果栈底指针指向空
exit(0);
s->top=s->base; //空栈,使栈底与栈顶指针相同
s->size=STACK_INIT_SIZE;
return s;
}
void DestroyStack(STACK *s) //销毁一个栈
{
free(s->base);
free(s);
}
int Push(STACK *s,ElemType *e) //压栈
{
if(s==NULL||e==NULL) //判断传入的参数是否合法
return 0;
if(s->top-s->base>=s->size)//如果满栈
{
s->base=(ElemType*)realloc(s->base,
(s->size+STACK_INCREME)*sizeof(ElemType));//重新分配栈的大小
if(s->base==NULL)//如果分配失败,返回零
return 0;
s->top=s->base+s->size;//重置栈顶指针
s->size=s->size+STACK_INCREME;//重置栈大小
}
/*
//写法一
*s->top=*e;//将数据存到栈顶
s->top++; //栈顶上移
*/
//写法二
*s->top++=*e;
return 1;
}
int Pop(STACK *s,ElemType *e) //出栈
{
if(s==NULL||e==NULL)//判断传入的参数是否合法
return 0;
if(s->base==s->top) return 0; //如果是空栈,返回
*e= *--s->top; //将栈顶元素存到*e中
return 1;
}
int IsEmpty(STACK *s) //判断栈是否为空
{
return s->top==s->base ? 1:0;
}
查找二叉树
tree.h
//tree.h
#ifndef _TREE_H
#define _TREE_H
typedef int ElemType;
typedef struct treenode
{
ElemType data;
struct treenode *left;
struct treenode *right;
}TREE;
TREE *MakeEmptyTree();
TREE *InsertTreeNode(ElemType e,TREE *t);
TREE *FindTreeNode(ElemType e,TREE *t);
TREE *FindMax(TREE *t);
TREE *FindMin(TREE *t);
TREE *DeleteTreeNode(ElemType e,TREE *t);
void DeleteTree(TREE **t);
#endif
tree.c
//tree.c
#include <stdio.h>
#include <stdlib.h>
#include "tree.h"
TREE *MakeEmptyTree() //创建一个空树
{
return NULL;
}
TREE *InsertTreeNode(ElemType e,TREE *t) //插入树结点
{
if(t==NULL) //如果是空树
{
t=(TREE *)malloc(sizeof(TREE));
if(t==NULL) return NULL; //如果没分配成功
t->data=e;
t->left=t->right=NULL;
}
else if(e<t->data) //如果小于树结点
{
t->left=InsertTreeNode(e,t->left); //插入树左边
}
else //否则
t->right=InsertTreeNode(e,t->right); //插入树右边
return t;
}
TREE *FindTreeNode(ElemType e,TREE *t) //查找结点
{
if(t==NULL) return NULL; //如果树为空
if(t->data==e) //如果查找的是根结点
return t;
else if(t->data<e) //大于根
return FindTreeNode(e,t->right);//去右边找
else //否则
return FindTreeNode(e,t->left); //去左边找
}
TREE *FindMax(TREE *t) //查找树的最大值
{
if(t==NULL) //如果是空树
return NULL;
if(t->right==NULL) //如果右子树为空
return t;
return FindMax(t->right); //否向右边找
}
TREE *FindMin(TREE *t) //查找树的最小值
{
if(t==NULL) return NULL; //如果树为空
if(t->left==NULL) //如果左子树为空
return t;
return FindMin(t->left); //否则向左边找
}
TREE *DeleteTreeNode(ElemType e,TREE *t)
{
TREE *p=NULL;
if(t==NULL) return NULL; //如果树为空
if(t->data>e) //小于根
t->left=DeleteTreeNode(e,t->left); //去左边删除
else if(t->data<e) //大于根
t->right=DeleteTreeNode(e,t->right);//去右边删除
else if(t->left && t->right) //当等于当前结点,且其左右子树均不为空
{
p=FindMin(t->right);//查找右子树的最小值
t->data=p->data; //将右子树的数据赋给当前找到的结点
t->right=DeleteTreeNode(t->data,t->right);
//到结点的右子树去删除数据为最小值的那个结点,并将删除之后的结果赋给右子树
}
else //当等于当前结点,且其左右子树有空
{
if(t->left==NULL)//如果左子树为空
t=t->right;//将右子树取代找到的结点
else if(t->right==NULL)//如果右子树为空
t=t->left;//将左子树取代找到的结点
free(t);//释放找到的结点
return NULL;
}
return t;
}
void DeleteTree(TREE **t) //删除整棵树
{
if(*t==NULL)
return ;
DeleteTree(&(*t)->left);
DeleteTree(&(*t)->right);
free(*t);
*t=NULL;
}
test.c
//test.c
#include <stdio.h>
#include <stdlib.h>
#include "tree.h"
void main()
{
int n;
TREE *p,*tree=MakeEmptyTree();
while(1)
{
printf("Please enter a num:");
fflush(stdin);
if(scanf("%d",&n)!=1)
break;
if(n==0)
break;
tree=InsertTreeNode(n,tree);
}
printf("Max of tree is %d,Min of tree is %d\n",
FindMax(tree)->data,FindMin(tree)->data);
fflush(stdin);
printf("Please enter search num:");
scanf("%d",&n);
if(FindTreeNode(n,tree))
printf("find %d\n",n);
else
printf("not find\n");
p=DeleteTreeNode(n,tree);
if(p)
printf("delete %d success\n",n);
else
printf("delete fail\n");
DeleteTree(&tree);
if(tree==NULL)
printf("delete success\n");
else
printf("delete faile\n");
}
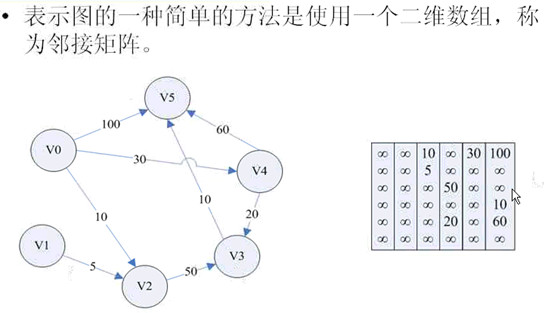
图
demo中的图结构
main.c
//main.c
#include<stdio.h>
#define MAX 10000
#define N 6
int G[N][N]=
{
{MAX,MAX,10,MAX,30,100}, //表示v0分别到各个顶点的距离
{MAX,MAX,5,MAX,MAX,MAX}, //表示v1分别到各个顶点的距离
{MAX,MAX,MAX,50,MAX,MAX},//表示v2分别到各个顶点的距离
{MAX,MAX,MAX,MAX,MAX,10},//表示v3分别到各个顶点的距离
{MAX,MAX,MAX,20,MAX,60}, //表示v4分别到各个顶点的距离
{MAX,MAX,MAX,MAX,MAX,MAX}//表示v5分别到各个顶点的距离
}; //图的矩阵图,行标表示起始顶点,列标表示终止顶点
int p[N][N]=
{
{0,0,0,0,0,0},//第1行表示v0到v0所需要经过的路径的顶点
{0,0,0,0,0,0},//第2行表示v0到v1
{0,2,0,0,0,0},//第3行表示v0到v2,因为v0能直接到达v2,则直接在第2列上填2,第1表示v0本身
{0,0,0,0,0,0},//第4行表示v0到v3
{0,4,0,0,0,0},//第5行表示v0到v4,因为v0能直接到达v4,则直接在第2列上填4
{0,5,0,0,0,0} //第6行表示v0到v5,因为v0能直接到达v5,则直接在第2列上填5
}; //用于存放第1个顶点到达其它顶点的最短距离经过的路径
//能从v0直接到达的初始化时写上,如上
void main()
{
int d[N]={MAX,MAX,10,MAX,30,100};//表示v0分别到各个顶点的距离
int flag[N]={0};
int i,v,min,k;
for(i=1;i<N;i++) //找出(第1个顶点到第i个顶点)的最短距离
{
min=MAX;
for(k=0,v=0;k<N;k++) //循环比较
{
if(flag[k]!=1 && min>d[k])
//如果(第1个顶点到第k个顶点)的最短距离没有比较过,且min大于(第1个顶点到第k个顶点)的最短距离
{
min=d[k]; //将(第1个顶点到第k个顶点)的最短距离的值赋给min
v=k; //将下标k存到v中
}
}//循环全部比较出来之后
flag[v]=1;//每循环1次,将flag[v]置1表示(第1个顶点到第v个顶点)的最短距离已经比较过了
d[v]=min;//将比较后的(第1顶点到第v个顶点)的直接最小距离存到d[v]中
for(k=0;k<N;k++) //循环比较,找出(第1个顶点到第k个顶点)最小的间接距离
{
if(flag[k]!=1 && min+G[v][k]<d[k]) //当存在间接距离小于直接距离
//
{
d[k]=min+G[v][k]; //则把间接距离赋给d[k]
if(p[k][0]==0)//如果原来没有被设置过
{
p[k][0]=1;
p[k][1]=v;//经过第v个顶点,将v设置到第2列
p[k][2]=k;//将k设置到第3列
}
else //否则,即p[v][i]原来被设置过
{
i=1;
while(p[v][i])//
{
p[k][i]=p[v][i];//将新得到的间接顶点设置到原来的最终顶点上
i++;//
}
p[k][i]=k;//将最终的顶点设置到p[k][i]
}
}
}
}
for(i=0;i<N;i++) //这个循环打印v0到其它顶点的最小出距离
printf("%5d",d[i]);
printf("\n\n");
for(i=1;i<N;i++) //这个循环打印v0到其它顶点经过的结点顺序
{
printf("v0-->v%d:::",i);
for(v=1;v<N;v++)
{
printf("%5d",p[i][v]);
}
printf("\n");
}
}