二分搜索
二分搜索
二分搜索是一种用于在已排序的数组中查找元素位置的搜索算法。在这种方法中,总是在数组一部分的中间搜索元素。
二分搜索的工作流程
二分搜索可以使用迭代与递归两种方式实现。
-
假设有如下1个排序数组,设
x=4为要搜索的元素;
-
分别在最低位与最高位设置低、高两个指针;

-
查找数组的中间元素
mid,例如:arr[(low + high)/2] = 6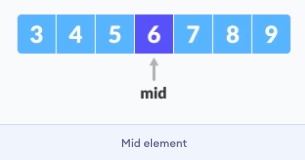
- 如果
x == mid,则返回mid,否则,将要搜索的元素与mid进行比较; - 如果
x > mid,则将x与mid右侧元素的中间元素进行比较, 这是通过将low设置为low = mid + 1来完成的; -
否则,将
x与mid左侧元素的中间元素进行比较,这是通过将high设置为high = mid - 1来完成的; -
重复步骤 3 到 6,走到高低相遇;

- 最终找到
x=4;
复杂度
|Time Complexity|| |—|—| |Best | O(1) | |Worst | O(log n) | |Average | O(log n) | |Space Complexity | O(1) | |Stability | No |
代码实现
Swift实现
//迭代方式
func iterateBinarySearch(array:[Int], x:Int, low:inout Int, high:inout Int) -> Int {
let mid = low + (high - low)/2
while low < high {
if array[mid] == x {
return mid
}else if array[mid] < x {
low = mid + 1
}else if array[mid] > x {
high = mid - 1
}
}
return -1
}
//递归方式
func recursiveBinarySearch(array:[Int], x:Int, low:inout Int, high:inout Int) -> Int {
if low <= high {
var mid = low + (high - low)/2
if array[mid] == x {
return mid
}else if array[mid] > x {
high = mid - 1
return recursiveBinarySearch(array: array, x: x, low: &low, high: &high)
}else if array[mid] < x {
low = mid + 1
return recursiveBinarySearch(array: array, x: x, low: &low, high: &high)
}
}
return -1
}
//打印
func printBinarySearch(){
let array:[Int] = [10, 11, 12, 13, 14, 15, 15, 17, 18, 111]
var low = 0
var high = array.count-1
let x = 14
//let index = iterateBinarySearch(array: array,x:x,low:&low,high:&high)
let index = recursiveBinarySearch(array: array,x:x,low:&low,high:&high)
print("==== \(x) 的index: \(index)")
}
Python 实现
# Binary Search in python
def binarySearch(array, x, low, high):
# Repeat until the pointers low and high meet each other
while low <= high:
mid = low + (high - low)//2
if array[mid] == x:
return mid
elif array[mid] < x:
low = mid + 1
else:
high = mid - 1
return -1
array = [3, 4, 5, 6, 7, 8, 9]
x = 4
result = binarySearch(array, x, 0, len(array)-1)
if result != -1:
print("Element is present at index " + str(result))
else:
print("Not found")
Java 实现
// Binary Search in Java
class BinarySearch {
int binarySearch(int array[], int x, int low, int high) {
// Repeat until the pointers low and high meet each other
while (low <= high) {
int mid = low + (high - low) / 2;
if (array[mid] == x)
return mid;
if (array[mid] < x)
low = mid + 1;
else
high = mid - 1;
}
return -1;
}
public static void main(String args[]) {
BinarySearch ob = new BinarySearch();
int array[] = { 3, 4, 5, 6, 7, 8, 9 };
int n = array.length;
int x = 4;
int result = ob.binarySearch(array, x, 0, n - 1);
if (result == -1)
System.out.println("Not found");
else
System.out.println("Element found at index " + result);
}
}
C 实现
// Binary Search in C
#include <stdio.h>
int binarySearch(int array[], int x, int low, int high) {
// Repeat until the pointers low and high meet each other
while (low <= high) {
int mid = low + (high - low) / 2;
if (array[mid] == x)
return mid;
if (array[mid] < x)
low = mid + 1;
else
high = mid - 1;
}
return -1;
}
int main(void) {
int array[] = {3, 4, 5, 6, 7, 8, 9};
int n = sizeof(array) / sizeof(array[0]);
int x = 4;
int result = binarySearch(array, x, 0, n - 1);
if (result == -1)
printf("Not found");
else
printf("Element is found at index %d", result);
return 0;
}
C++ 实现
// Binary Search in C++
#include <iostream>
using namespace std;
int binarySearch(int array[], int x, int low, int high) {
// Repeat until the pointers low and high meet each other
while (low <= high) {
int mid = low + (high - low) / 2;
if (array[mid] == x)
return mid;
if (array[mid] < x)
low = mid + 1;
else
high = mid - 1;
}
return -1;
}
int main(void) {
int array[] = {3, 4, 5, 6, 7, 8, 9};
int x = 4;
int n = sizeof(array) / sizeof(array[0]);
int result = binarySearch(array, x, 0, n - 1);
if (result == -1)
printf("Not found");
else
printf("Element is found at index %d", result);
}