堆排序
堆排序
堆排序是指利用堆这种数据结构所设计的一种排序算法,基于数组与树两种数据结构。因为堆是一个近似完全二叉树的结构,并且子结点的键值或索引总是小于(或者大于)它的父节点。

堆排序其实就是利用堆的概念来排序的选择排序,原理是将数组的元素可视化为一种特殊的完整二叉树,称为堆。堆分为两种: 最大堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列; 最小堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列; 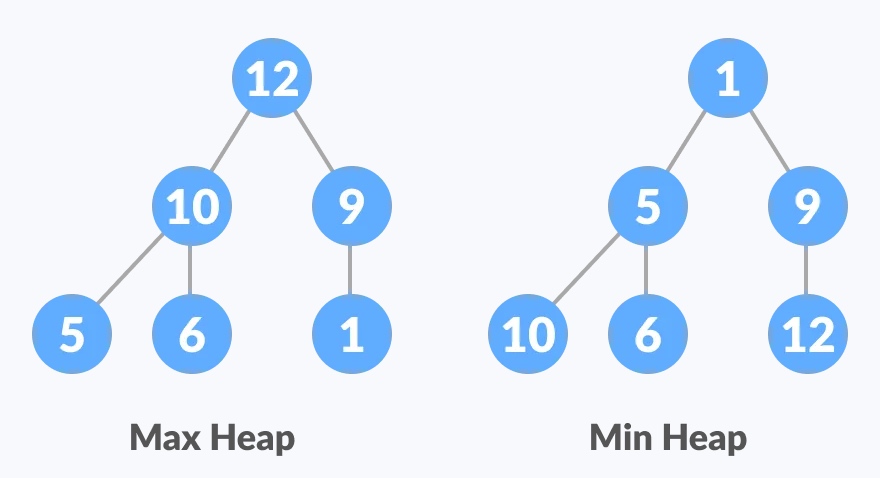
完整二叉树有一个有趣的特性,我们可以用它来找到任何节点的子节点和父节点。比如数组中任何一个索引为i的元素,则它的左子元素的索引为2i+1,右子元素的索引为2i+2。 此外,索引为i的元素的父元素的索引为(i-1)/2。 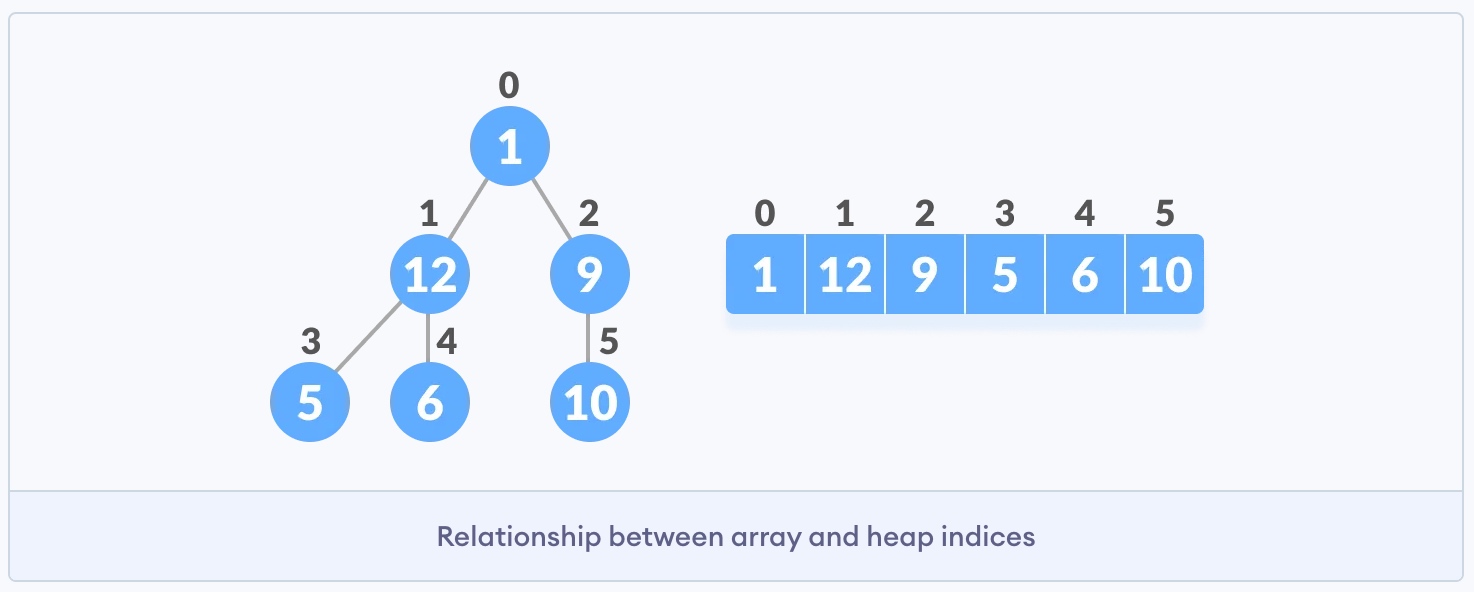
如何”堆化(heapify)”一颗树
堆化一颗树是通过在堆的所有非叶了节点上运行一个名为heapify的函数,将其修改为一个最大(小)堆。下面先以两个最基本的场景看Heapify过程:
Base case 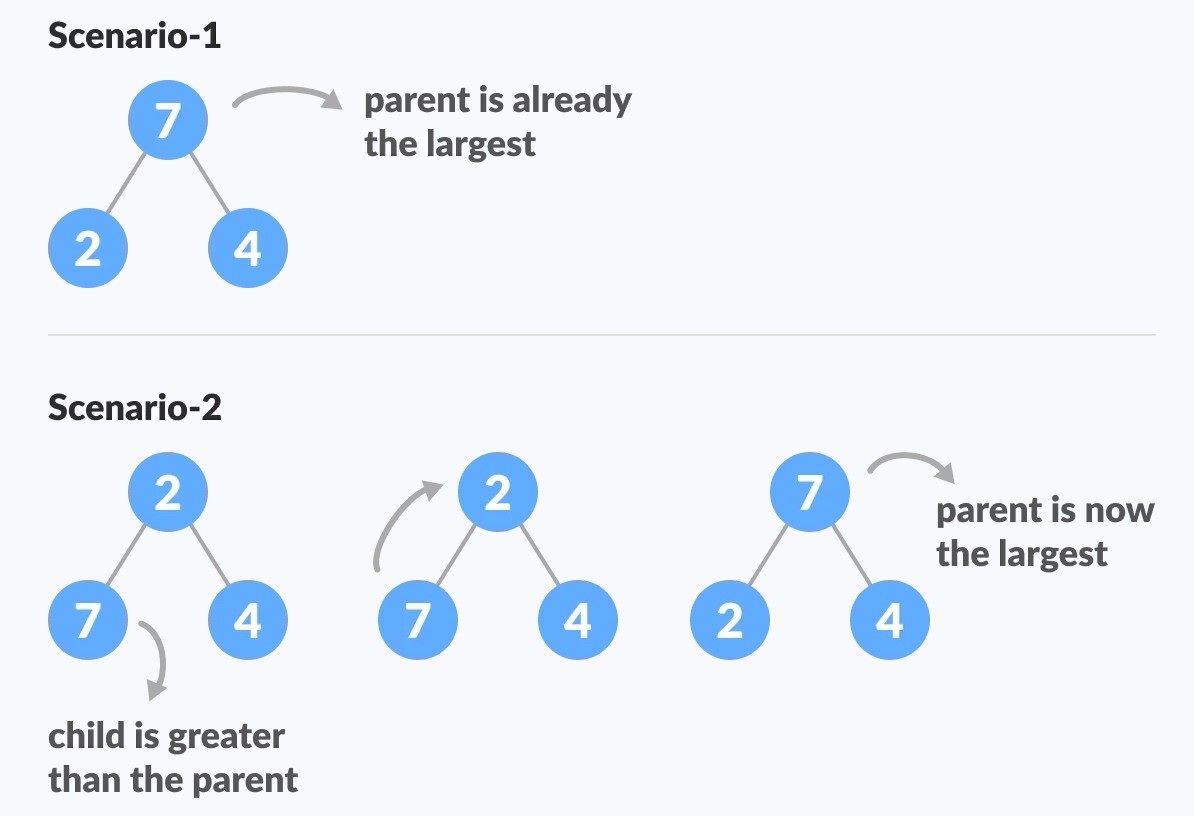 上图的 Scenario-1 中的根元素是最大的,说明已经是最大堆了,所以不需要做任何操作;Scenario-2 中有一个比根元素
上图的 Scenario-1 中的根元素是最大的,说明已经是最大堆了,所以不需要做任何操作;Scenario-2 中有一个比根元素2大的子元素7,所以这里需要交换以维持这个case的最大堆性质;
当节点不只一层,有子树的情况下 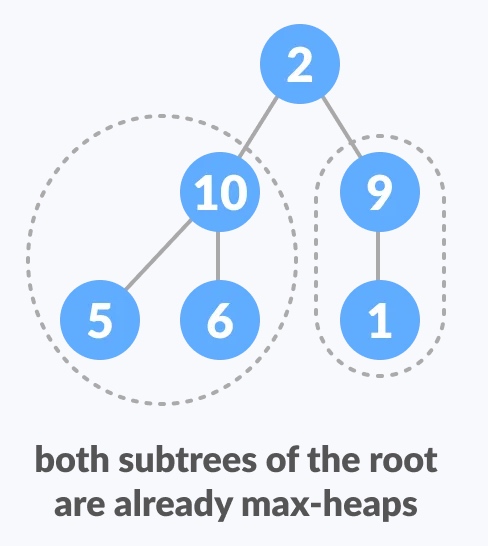 当只有顶部不是最大堆,而子树都是最大堆的情况下,要维护这颗树的最大值性质,就需要持续把
当只有顶部不是最大堆,而子树都是最大堆的情况下,要维护这颗树的最大值性质,就需要持续把2往下层推直到它到达正确位置。操作过程如下: 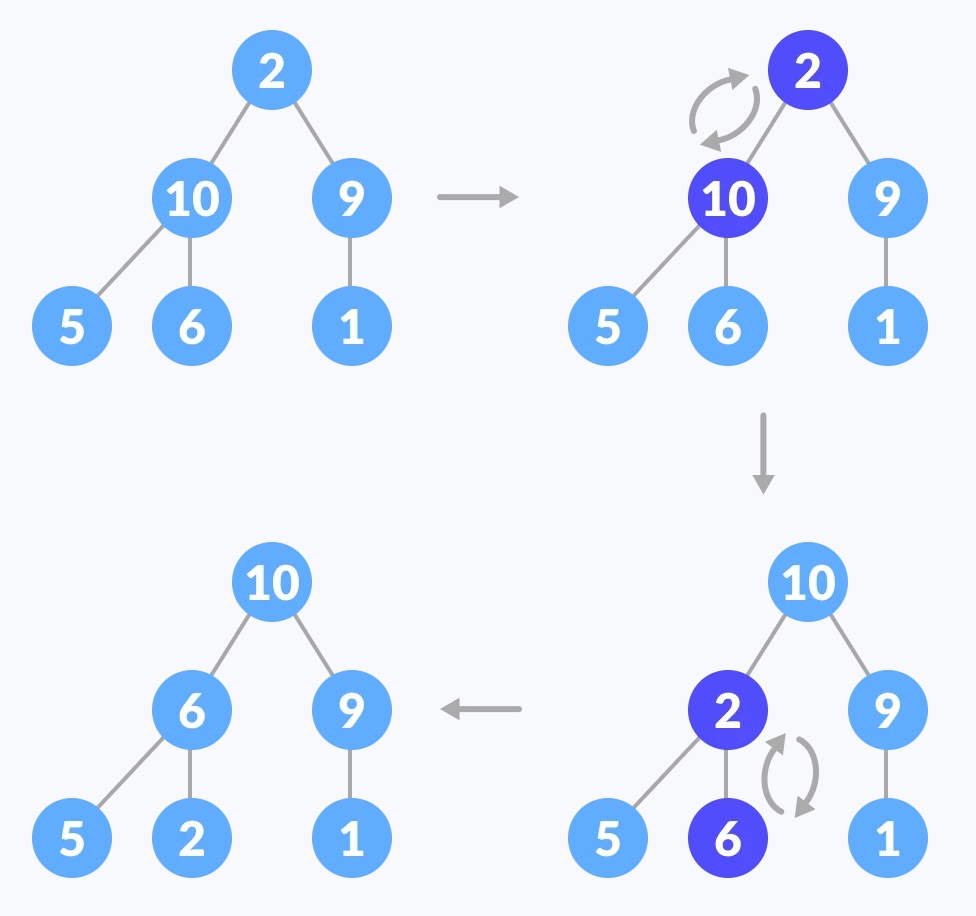 因此,要在两个子树都是最大堆的树中维护最大堆的性质,就需要对根元素重复运行
因此,要在两个子树都是最大堆的树中维护最大堆的性质,就需要对根元素重复运行heapify,直到它大于其子节点或成为叶节点。
构造最大堆(max-heap)
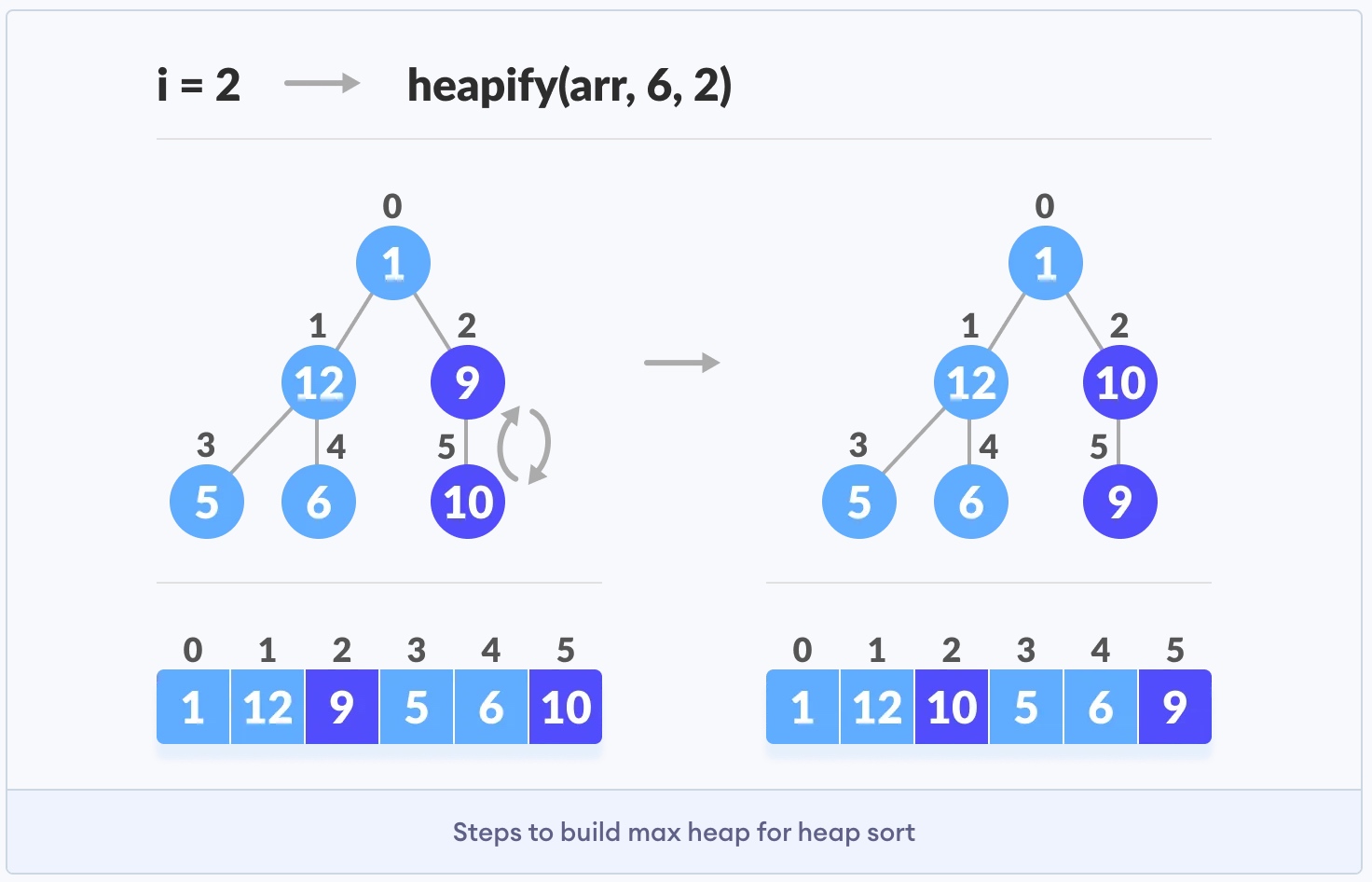
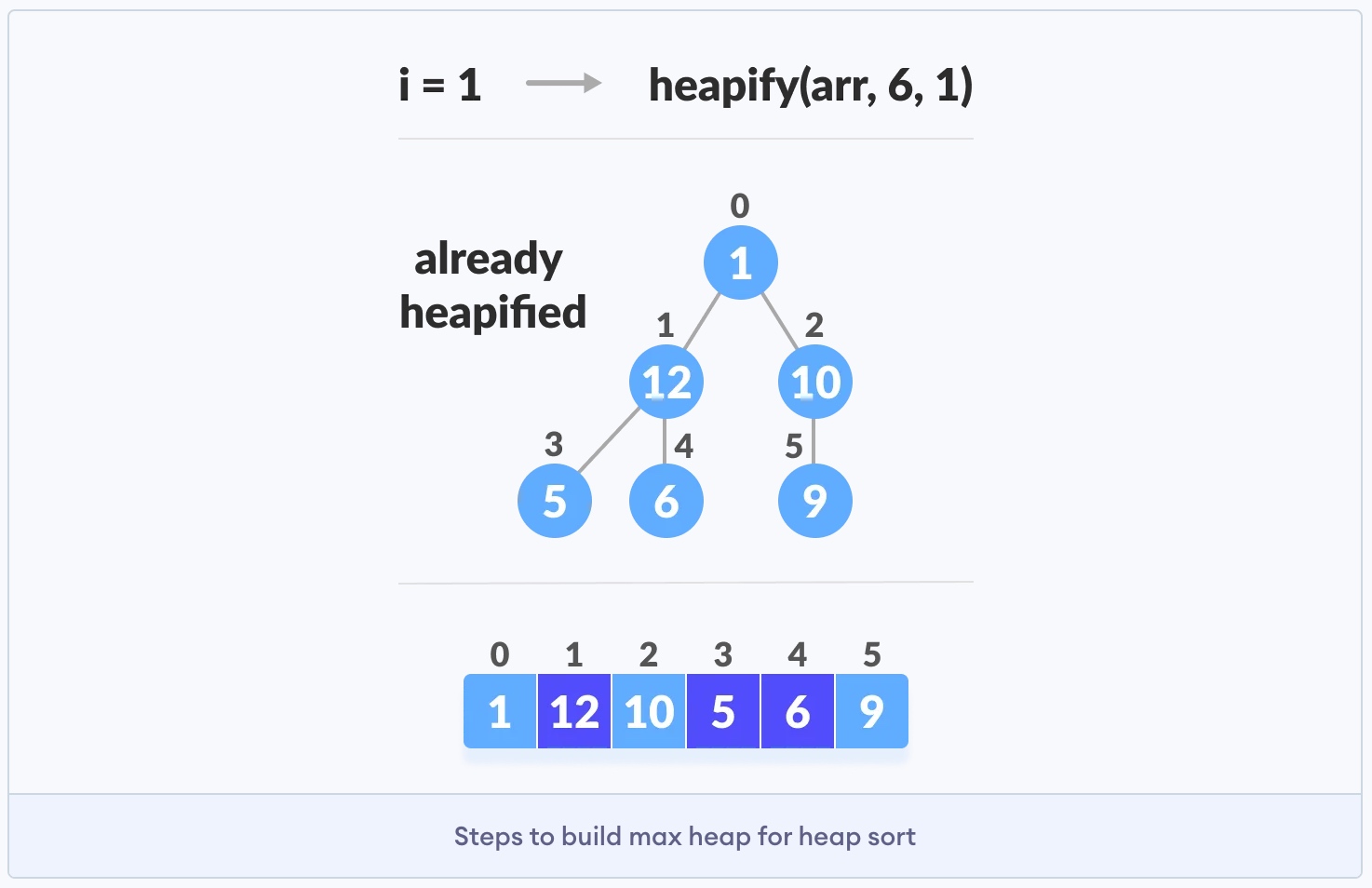
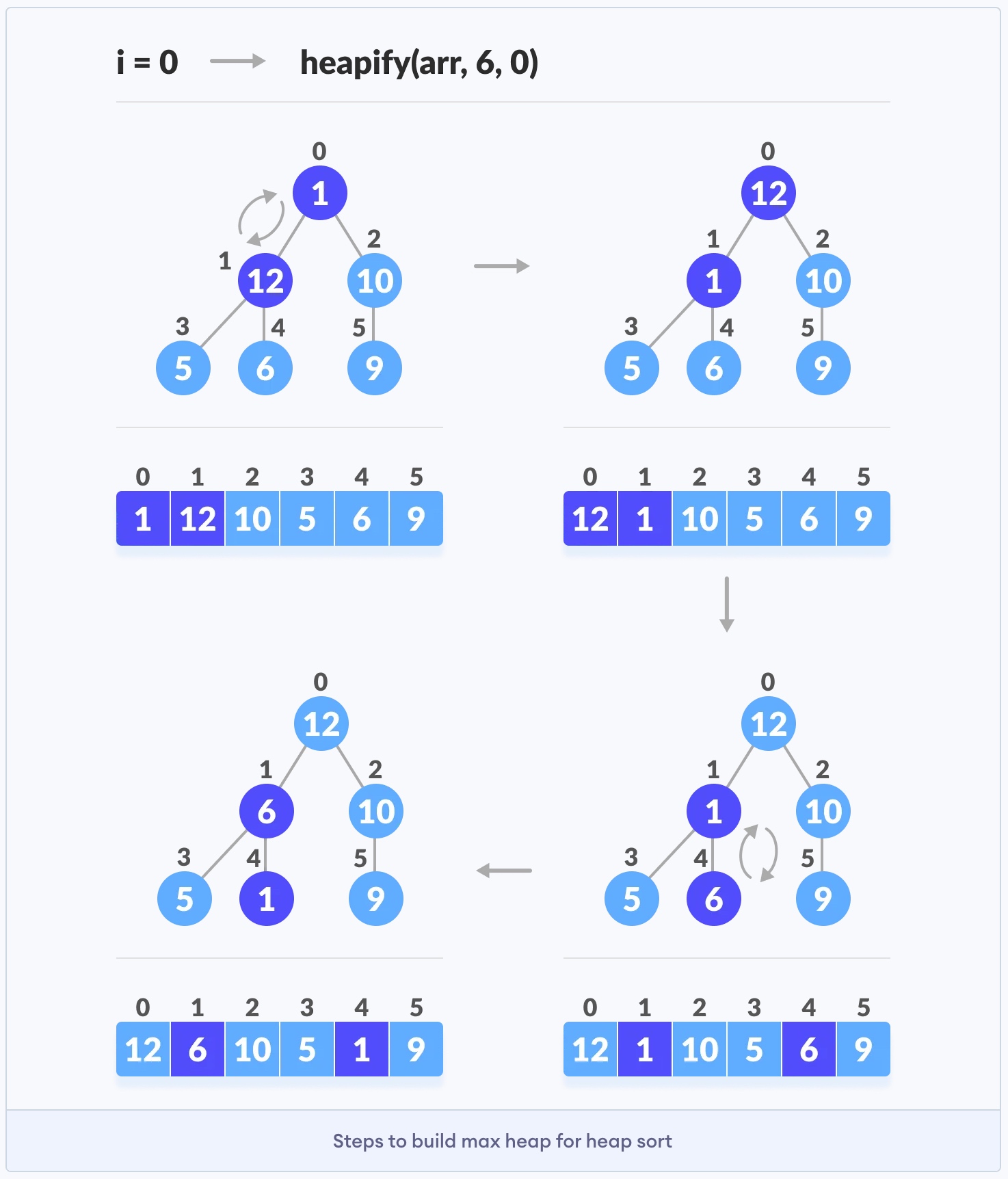
从任何树构建最大堆,可以从底向上开始堆化它的每个子树,并在将heapify函数应用于包括根元素在内的所有元素,最后以形成最大堆结束。
对于完整二叉树,第一个非叶节点的索引在n/2 - 1,此索引之后的所有其他节点都是叶节点,因此不需要堆化heapify。由此,我们可以这样去建立一个最大堆:
// Build heap (rearrange array)
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);

堆排序的工作流程
- 由于树满足最大堆(Max-Heap)性质,所以最大的元素存储在根节点;
- Swap:取出根元素,放在数组的末尾(第n个位置)把树(堆)的最后一项放在空的地方。
- Remove:将堆的大小减少1。
- Heapify:再次对根元素进行Heapify,使我们在根处获得最大元素。
- 重复该过程,直到列表中的所有项目都排序完毕。
过程如下: 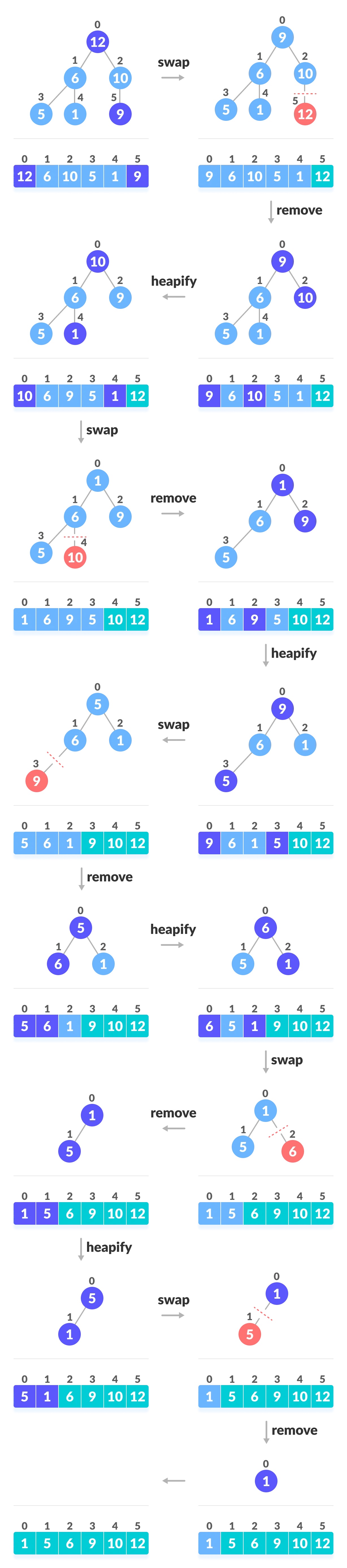 这个操作过程代码如下:
这个操作过程代码如下:
// Heap sort
for (int i = n - 1; i >= 0; i--) {
swap(&arr[0], &arr[i]);
// Heapify root element to get highest element at root again
heapify(arr, i, 0);
}
复杂度
|Time Complexity|| |—|—| |Best | O(nlog n) | |Worst | O(nlog n) | |Average | O(nlog n) | |Space Complexity | O(1) | |Stability | No |
代码实现
Swift实现
import Foundation
//参考:https://www.programiz.com/dsa/heap-sort
func heapSort(array:inout [Int]) {
//构建最大堆,从完全二叉树的最后一个非叶子节点往前作堆化;最后一个非叶节点的索引是:(n/2 - 1)
var i = array.count/2 - 1
while i >= 0 {
//堆化
heapify(array: &array, n: array.count, i: i)
i -= 1
}
//堆排序,遍历所有的节点,依次拿根节点的值与它互换;
//因为每次取根节点的值互换后都会重新堆化,所以每次取的值都是新堆里最大的,当迭代完成后其实就完成了数组的重排
var j = array.count - 1
while j >= 0 {
//值互换,依次把根节点值交换到非叶子节点处
array.swapAt(0, j)
//在大小为j的堆上再次做堆化处理,以期下次在根位置(0)处获得的值,仍然是这个大小为j的堆里最大的
heapify(array: &array, n: j, i: 0)
j -= 1
}
}
//堆化,是自顶向下(从根到叶子)把底层的大值交换到顶层的迭代过程
func heapify(array:inout [Int], n:Int, i:Int) {
//假设默认i指向是当前堆的最大值,定义一个largest指针指向最大值
var largest: Int = i
//则左右孩子指针分别为left、right
let left = 2 * i + 1
let right = 2 * i + 2
//如果左指针left在当前堆大小n的范围内,并且left所指的值大于前最大值
if left < n && array[left] > array[largest] {
largest = left //赋值largest指向左指针位置,largest指向发生变化
}
//如果右指针right在当前堆大小n的范围内,并且right所指的值大于前最大值
if right < n && array[right] > array[largest] {
largest = right //赋值largest指向右指针位置,largest指向发生变化
}
//如果largest指向发生变化,不再是默认i指的位置了
if largest != i {
//交换array[i]与array[largest]的值
array.swapAt(i, largest) //因i是left与right的父节点,这个交换操作保证了父节点的值大于子节点的
//因为在这个if里largest是已经被赋值指向了子节点,所以继续递归对子节点作堆化处理
heapify(array: &array, n: n, i: largest)
}
}
//打印
func printHeapSortSort(_ array:inout [Int]){
heapSort(array: &array)
print(array)
}
var arr:[Int] = [3, 2, 5, 7, 1, 5, 4, 8, 11, 0]
printHeapSortSort(&arr)
Python 实现
# Heap Sort in python
def heapify(arr, n, i):
# Find largest among root and children
largest = i
l = 2 * i + 1
r = 2 * i + 2
if l < n and arr[i] < arr[l]:
largest = l
if r < n and arr[largest] < arr[r]:
largest = r
# If root is not largest, swap with largest and continue heapifying
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)
def heapSort(arr):
n = len(arr)
# Build max heap
for i in range(n//2, -1, -1):
heapify(arr, n, i)
for i in range(n-1, 0, -1):
# Swap
arr[i], arr[0] = arr[0], arr[i]
# Heapify root element
heapify(arr, i, 0)
arr = [1, 12, 9, 5, 6, 10]
heapSort(arr)
n = len(arr)
print("Sorted array is")
for i in range(n):
print("%d " % arr[i], end='')
Java 实现
// Heap Sort in Java
public class HeapSort {
public void sort(int arr[]) {
int n = arr.length;
// Build max heap
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
// Heap sort
for (int i = n - 1; i >= 0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
// Heapify root element
heapify(arr, i, 0);
}
}
void heapify(int arr[], int n, int i) {
// Find largest among root, left child and right child
int largest = i;
int l = 2 * i + 1;
int r = 2 * i + 2;
if (l < n && arr[l] > arr[largest])
largest = l;
if (r < n && arr[r] > arr[largest])
largest = r;
// Swap and continue heapifying if root is not largest
if (largest != i) {
int swap = arr[i];
arr[i] = arr[largest];
arr[largest] = swap;
heapify(arr, n, largest);
}
}
// Function to print an array
static void printArray(int arr[]) {
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
// Driver code
public static void main(String args[]) {
int arr[] = { 1, 12, 9, 5, 6, 10 };
HeapSort hs = new HeapSort();
hs.sort(arr);
System.out.println("Sorted array is");
printArray(arr);
}
}
C 实现
// Heap Sort in C
#include <stdio.h>
// Function to swap the the position of two elements
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
void heapify(int arr[], int n, int i) {
// Find largest among root, left child and right child
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left < n && arr[left] > arr[largest])
largest = left;
if (right < n && arr[right] > arr[largest])
largest = right;
// Swap and continue heapifying if root is not largest
if (largest != i) {
swap(&arr[i], &arr[largest]);
heapify(arr, n, largest);
}
}
// Main function to do heap sort
void heapSort(int arr[], int n) {
// Build max heap
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
// Heap sort
for (int i = n - 1; i >= 0; i--) {
swap(&arr[0], &arr[i]);
// Heapify root element to get highest element at root again
heapify(arr, i, 0);
}
}
// Print an array
void printArray(int arr[], int n) {
for (int i = 0; i < n; ++i)
printf("%d ", arr[i]);
printf("\n");
}
// Driver code
int main() {
int arr[] = {1, 12, 9, 5, 6, 10};
int n = sizeof(arr) / sizeof(arr[0]);
heapSort(arr, n);
printf("Sorted array is \n");
printArray(arr, n);
}
C++ 实现
// Heap Sort in C++
#include <iostream>
using namespace std;
void heapify(int arr[], int n, int i) {
// Find largest among root, left child and right child
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left < n && arr[left] > arr[largest])
largest = left;
if (right < n && arr[right] > arr[largest])
largest = right;
// Swap and continue heapifying if root is not largest
if (largest != i) {
swap(arr[i], arr[largest]);
heapify(arr, n, largest);
}
}
// main function to do heap sort
void heapSort(int arr[], int n) {
// Build max heap
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
// Heap sort
for (int i = n - 1; i >= 0; i--) {
swap(arr[0], arr[i]);
// Heapify root element to get highest element at root again
heapify(arr, i, 0);
}
}
// Print an array
void printArray(int arr[], int n) {
for (int i = 0; i < n; ++i)
cout << arr[i] << " ";
cout << "\n";
}
// Driver code
int main() {
int arr[] = {1, 12, 9, 5, 6, 10};
int n = sizeof(arr) / sizeof(arr[0]);
heapSort(arr, n);
cout << "Sorted array is \n";
printArray(arr, n);
}