基数排序
基数排序
< 基数排序是首先对相同位值的各个数字进行分组来对元素进行排序。 然后,根据元素的递增/递减顺序对元素进行排序。
原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。

三种利用了桶的概念的排序算法:
基数排序:根据键值的每位数字来分配桶; 计数排序:每个桶只存储单一键值; 桶排序:每个桶存储一定范围的数值;
下图所示对数组为 [121, 432, 564, 23, 1, 45, 788] 按照基数排序。 
基数排序的工作流程
-
从数组中找出最大的数
max,然后令X为这个最大的数max的位数,并以X来确定后面循环的排序过程应该要到达的位置。比如说上面的数组中最大数为788有3数位(百、十、个),所以循环排序的过程要到达百位才能结束。 -
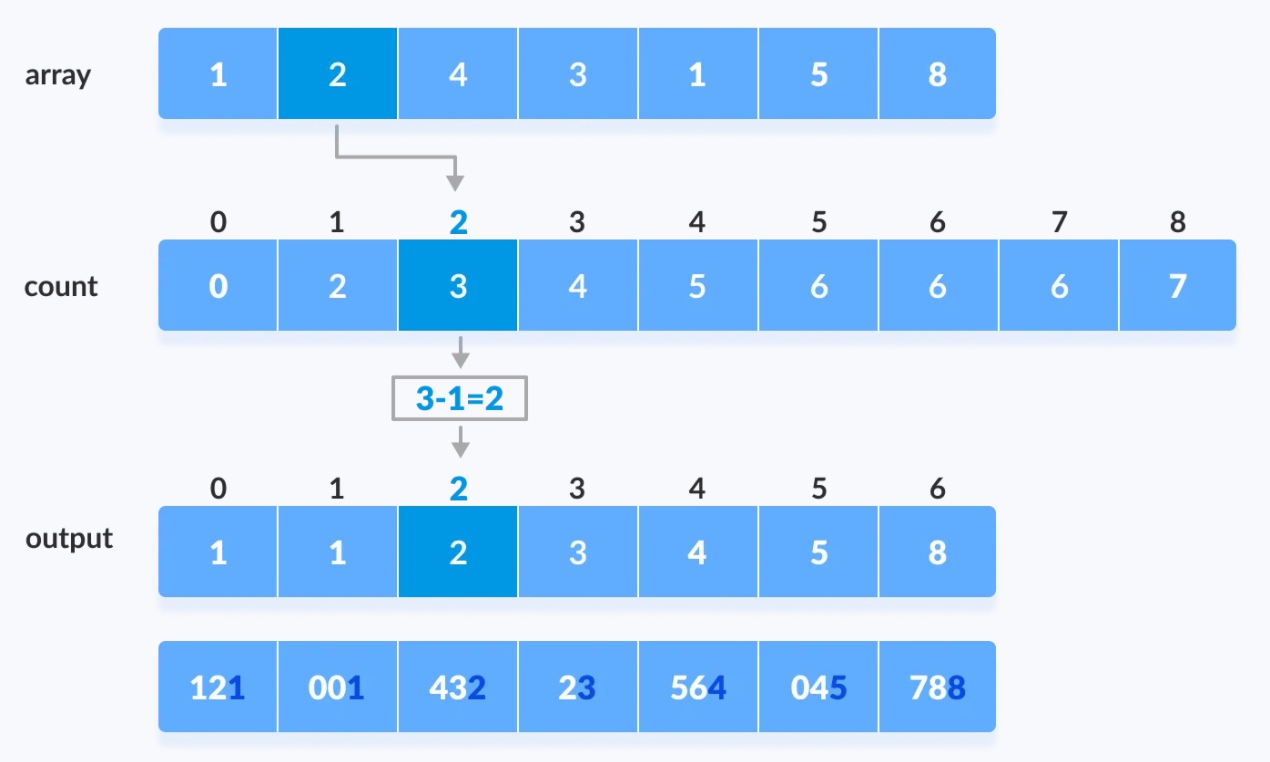
对数组中的数字对应位上的每个数字进行排序,这个排序可以使用任意一种稳定的排序算法。比如下面对数组的数字中的个位进行基数排序。
-
然后在原来的基础上对十位数进行排序。

-
最后在第3步排序后的基础上,再对百位数进行对数组中数字排序。

代码实现
Swift实现
// 基数排序首先通过对相同位值的各个数字进行分组来对元素进行排序。先对个位的数字排序、再排十位,一直到最高位。
// 而每组同位数字的排序可以使用任何稳定的排序技术进行排序。
import Foundation
//基数排序
func radixSort(array:inout [Int]){
if array.count == 0 {
return
}
//取最大值,确定基数的最大位数,进行遍历
let max = array.max() ?? 0
var place = 1
while max / place > 0 {
//作有基数位的计数排序
radixCountSort(array: &array, place: place)
place *= 10
}
}
//有基数位的计数排序,place代表基数位
func radixCountSort(array:inout [Int],place:Int) {
//获得数组中的最大值
let max = array.max() ?? 0
//定义一个大小为(max+1)的计数数组
var count = [Int](https://luowei.github.io/list/repeating: 0, count: max+1)
//先算每个元素(索引位置)的计数,得到元数的计数数组。以原数组值为索引,在count中存储这个值在原数组中出现的计数
for i in 0 ..< array.count {
count[(array[i] / place) % 10] += 1 //这里索引模 %10,所以有计数的索引在0-9
}
//再算每个元素(索引位置)的计数前缀累积和,得到一个索引计数的前缀和数组
for i in 1 ... 9 { //因为有计数的索引在0-9,所以遍历0-9
count[i] += count[i - 1]
}
//print("== cosum:\(count)")
//定义一个输出数组
var output = [Int](https://luowei.github.io/list/repeating: 0, count: array.count)
//count数组中的某个索引的累积和,代表这个索引对应元素应该在原数组中排在什么位置
//所以遍历原数组中每个元素,根据这个元素在count数组中的累积和,得出它应该排在数组中的 count[array[i]] - 1
// for i in 0 ..< array.count {
for i in stride(from: array.count - 1, through:0, by: -1) { //注意这里要倒序遍历,不然多次调用此排序方法顺序就不对了
output[count[(array[i] / place) % 10] - 1] = array[i]
count[(array[i] / place) % 10] -= 1
}
//将outpu拷贝到原数组
for i in 0 ..< array.count {
array[i] = output[i]
}
}
//打印
func printRadixCountSort(_ array:inout [Int]){
//var array:[Float] = [3, 2, 5, 7, 1, 5, 4, 8, 11, 0]
radixSort(array: &array)
print(array)
}
var arr:[Int] = [121, 432, 564, 23, 1, 45, 788]
printRadixCountSort(&arr)
Python实现
# Radix sort in Python
# Using counting sort to sort the elements in the basis of significant places
def countingSort(array, place):
size = len(array)
output = [0] * size
count = [0] * 10
# Calculate count of elements
for i in range(0, size):
index = array[i] // place
count[index % 10] += 1
# Calculate cumulative count
for i in range(1, 10):
count[i] += count[i - 1]
# Place the elements in sorted order
i = size - 1
while i >= 0:
index = array[i] // place
output[count[index % 10] - 1] = array[i]
count[index % 10] -= 1
i -= 1
for i in range(0, size):
array[i] = output[i]
# Main function to implement radix sort
def radixSort(array):
# Get maximum element
max_element = max(array)
# Apply counting sort to sort elements based on place value.
place = 1
while max_element // place > 0:
countingSort(array, place)
place *= 10
data = [121, 432, 564, 23, 1, 45, 788]
radixSort(data)
print(data)
Java实现
// Radix Sort in Java Programming
import java.util.Arrays;
class RadixSort {
// Using counting sort to sort the elements in the basis of significant places
void countingSort(int array[], int size, int place) {
int[] output = new int[size + 1];
int max = array[0];
for (int i = 1; i < size; i++) {
if (array[i] > max)
max = array[i];
}
int[] count = new int[max + 1];
for (int i = 0; i < max; ++i)
count[i] = 0;
// Calculate count of elements
for (int i = 0; i < size; i++)
count[(array[i] / place) % 10]++;
// Calculate cumulative count
for (int i = 1; i < 10; i++)
count[i] += count[i - 1];
// Place the elements in sorted order
for (int i = size - 1; i >= 0; i--) {
output[count[(array[i] / place) % 10] - 1] = array[i];
count[(array[i] / place) % 10]--;
}
for (int i = 0; i < size; i++)
array[i] = output[i];
}
// Function to get the largest element from an array
int getMax(int array[], int n) {
int max = array[0];
for (int i = 1; i < n; i++)
if (array[i] > max)
max = array[i];
return max;
}
// Main function to implement radix sort
void radixSort(int array[], int size) {
// Get maximum element
int max = getMax(array, size);
// Apply counting sort to sort elements based on place value.
for (int place = 1; max / place > 0; place *= 10)
countingSort(array, size, place);
}
// Driver code
public static void main(String args[]) {
int[] data = { 121, 432, 564, 23, 1, 45, 788 };
int size = data.length;
RadixSort rs = new RadixSort();
rs.radixSort(data, size);
System.out.println("Sorted Array in Ascending Order: ");
System.out.println(Arrays.toString(data));
}
}
C 实现
// Radix Sort in C Programming
#include <stdio.h>
// Function to get the largest element from an array
int getMax(int array[], int n) {
int max = array[0];
for (int i = 1; i < n; i++)
if (array[i] > max)
max = array[i];
return max;
}
// Using counting sort to sort the elements in the basis of significant places
void countingSort(int array[], int size, int place) {
int output[size + 1];
int max = (array[0] / place) % 10;
for (int i = 1; i < size; i++) {
if (((array[i] / place) % 10) > max)
max = array[i];
}
int count[max + 1];
for (int i = 0; i < max; ++i)
count[i] = 0;
// Calculate count of elements
for (int i = 0; i < size; i++)
count[(array[i] / place) % 10]++;
// Calculate cumulative count
for (int i = 1; i < 10; i++)
count[i] += count[i - 1];
// Place the elements in sorted order
for (int i = size - 1; i >= 0; i--) {
output[count[(array[i] / place) % 10] - 1] = array[i];
count[(array[i] / place) % 10]--;
}
for (int i = 0; i < size; i++)
array[i] = output[i];
}
// Main function to implement radix sort
void radixsort(int array[], int size) {
// Get maximum element
int max = getMax(array, size);
// Apply counting sort to sort elements based on place value.
for (int place = 1; max / place > 0; place *= 10)
countingSort(array, size, place);
}
// Print an array
void printArray(int array[], int size) {
for (int i = 0; i < size; ++i) {
printf("%d ", array[i]);
}
printf("\n");
}
// Driver code
int main() {
int array[] = {121, 432, 564, 23, 1, 45, 788};
int n = sizeof(array) / sizeof(array[0]);
radixsort(array, n);
printArray(array, n);
}
C++ 实现
// Radix Sort in C++ Programming
#include <iostream>
using namespace std;
// Function to get the largest element from an array
int getMax(int array[], int n) {
int max = array[0];
for (int i = 1; i < n; i++)
if (array[i] > max)
max = array[i];
return max;
}
// Using counting sort to sort the elements in the basis of significant places
void countingSort(int array[], int size, int place) {
const int max = 10;
int output[size];
int count[max];
for (int i = 0; i < max; ++i)
count[i] = 0;
// Calculate count of elements
for (int i = 0; i < size; i++)
count[(array[i] / place) % 10]++;
// Calculate cumulative count
for (int i = 1; i < max; i++)
count[i] += count[i - 1];
// Place the elements in sorted order
for (int i = size - 1; i >= 0; i--) {
output[count[(array[i] / place) % 10] - 1] = array[i];
count[(array[i] / place) % 10]--;
}
for (int i = 0; i < size; i++)
array[i] = output[i];
}
// Main function to implement radix sort
void radixsort(int array[], int size) {
// Get maximum element
int max = getMax(array, size);
// Apply counting sort to sort elements based on place value.
for (int place = 1; max / place > 0; place *= 10)
countingSort(array, size, place);
}
// Print an array
void printArray(int array[], int size) {
int i;
for (i = 0; i < size; i++)
cout << array[i] << " ";
cout << endl;
}
// Driver code
int main() {
int array[] = {121, 432, 564, 23, 1, 45, 788};
int n = sizeof(array) / sizeof(array[0]);
radixsort(array, n);
printArray(array, n);
}