归并排序
归并排序
归并排序是基于分而治之算法的原理。把一个问题被划分为多个独立的子问题,再对每个子问题作同样的划分,直到base case无法再分时处理base case问题即可。最后,将子问题一层层合并起来形成最终解决方案。
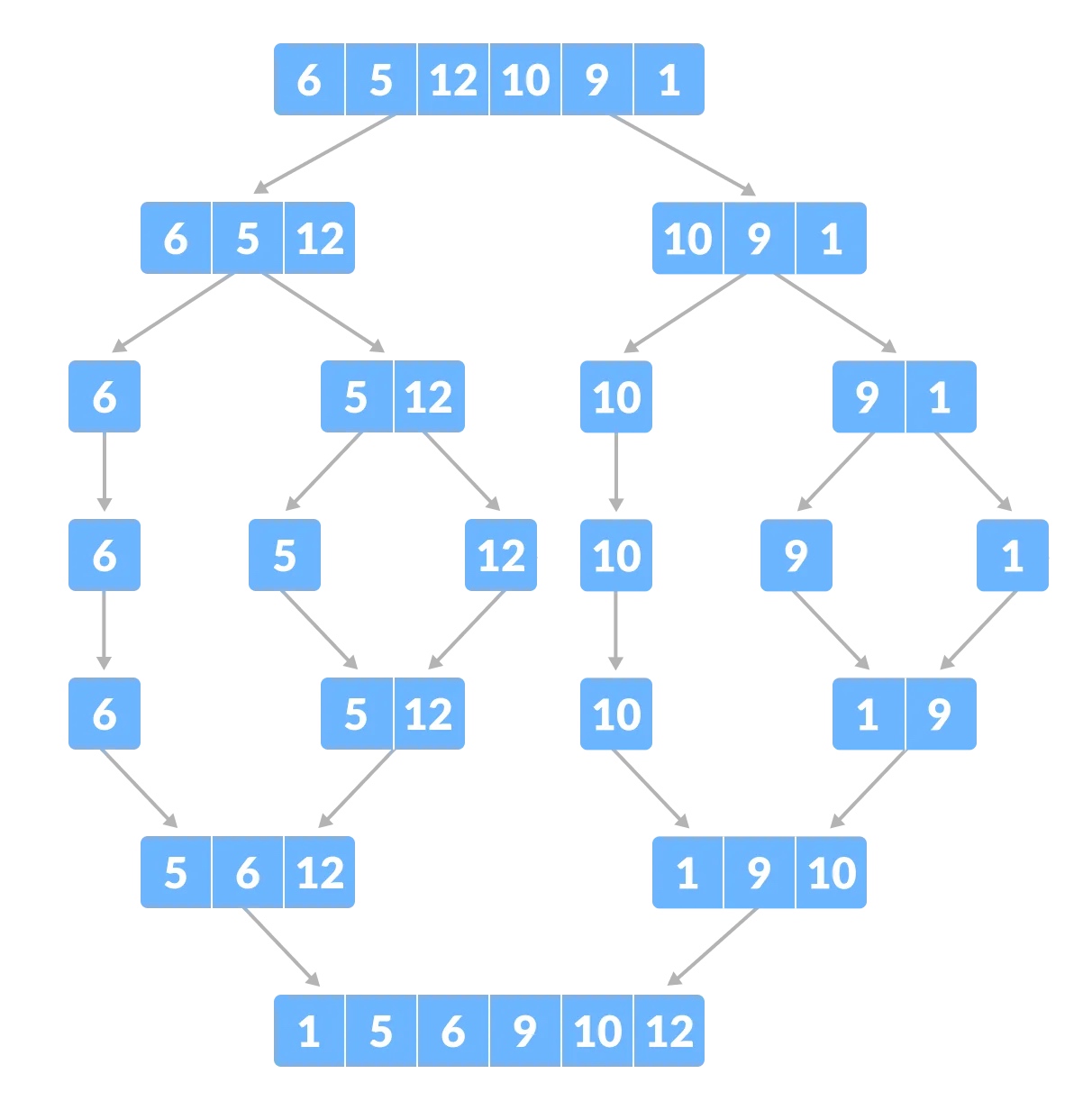
假设我们必须对数组 A 进行排序,定义一个子问题是对这个数组的一个子部分进行排序,例如从索引 p 开始到索引 r 结束,表示为 A[p..r]。

步骤
划分 如果 q 是 p 和 r 的中间点,那么我们可以将子数组 A[p..r] 拆分为两个数组 A[p..q] 和 A[q+1, r]。
处理 在处理步骤中,我们尝试对子数组 A[p..q] 和 A[q+1, r] 进行排序。 如果还没有达到base case,就再次划分这两个子数组并尝试对它们进行排序。
合并 当处理到达base step,并且我们得到数组 A[p..r] 的两个排序子数组 A[p..q] 和 A[q+1, r] 时,通过创建一个排序数组 A[p..r] 来合并来自两个已排序的子数组 A[p..q] 和 A[q+1, r]的结果。
图示合并的过程
以下数组 A[0..5] 包含两个已排序的子数组 A[0..3] 和 A[4..5] 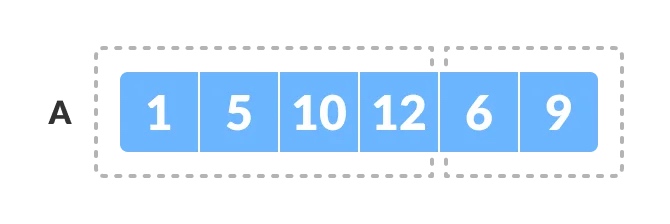
创建子数组的副本以进行合并 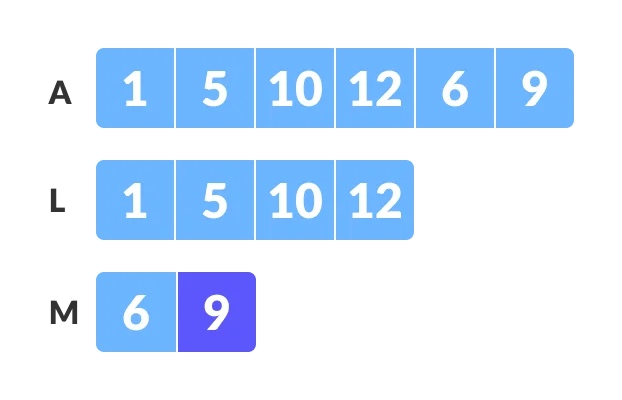
定义3个索引指针来操作子数组与合并的数组 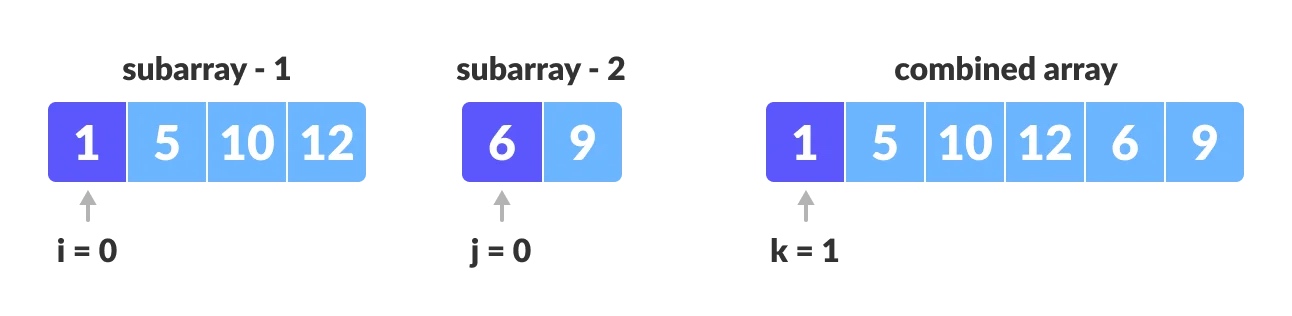
两数组合并过程 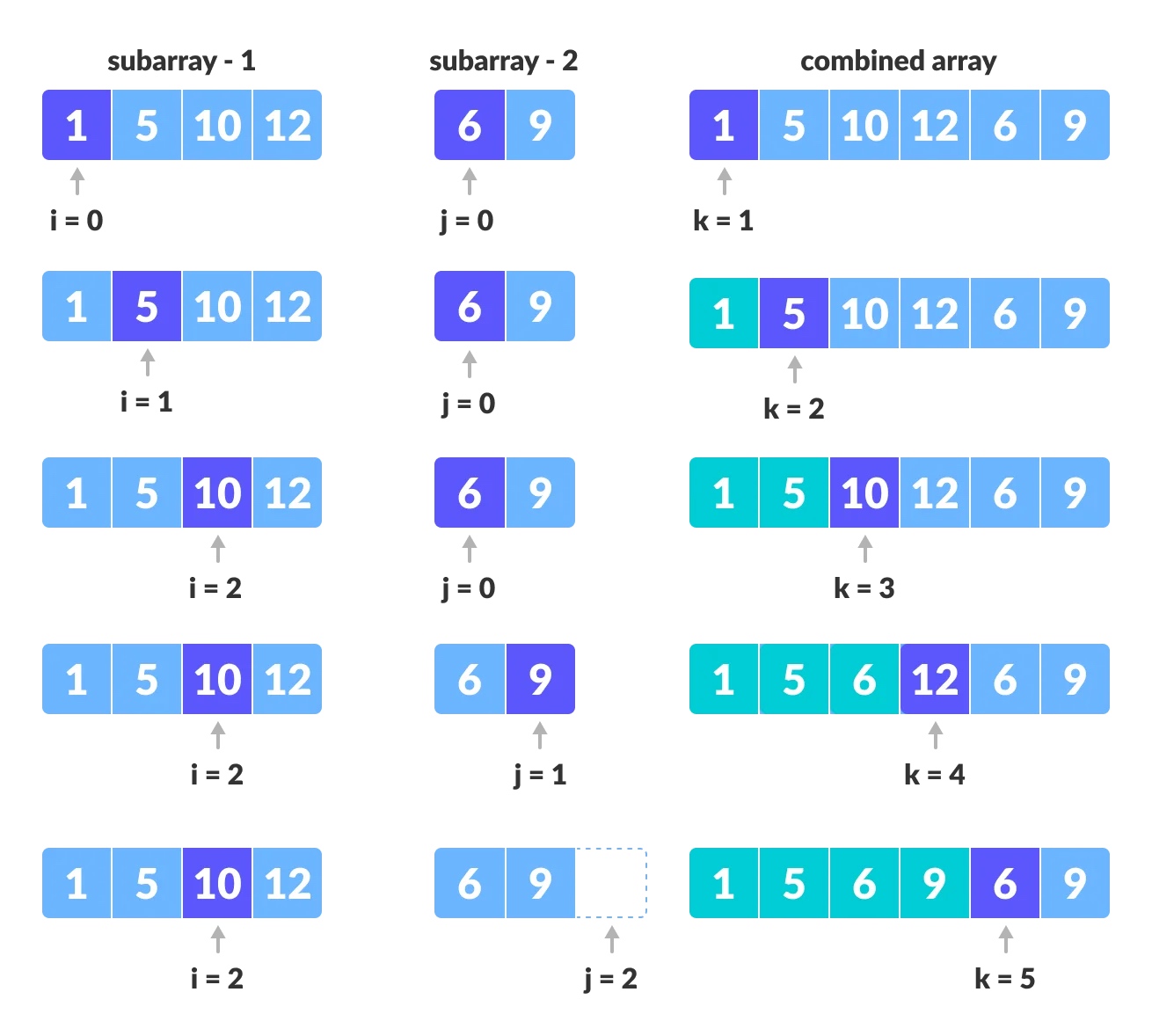
剩余元素追加的过程 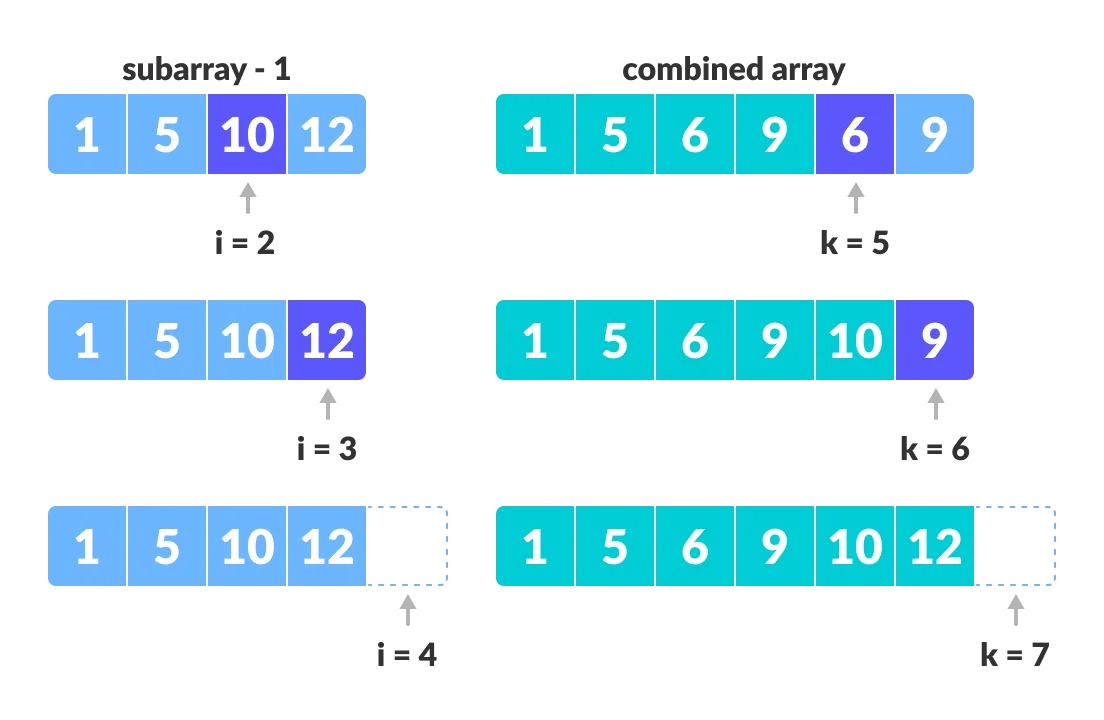

复杂度
|Time Complexity|| |—|—| |Best | O(nlog n) | |Worst | O(nlog n) | |Average | O(n*log n) | |Space Complexity | O(n) | |Stability | Yes |
代码实现
Swift 实现
import Foundation
//对数组在 l..r 区间的元素作归并排序,左闭右开
func mergeSort(array:inout [Int],l:Int,r:Int) {
if l < r {
//取中点,把在 l..r 区间的数组元素分成两个子数组
let m = l + (r - l) / 2
//对两个子数组分别作同样的归并排序
mergeSort(array: &array, l: l, r: m)
mergeSort(array: &array, l: m+1, r: r)
//合并已排好序的子数组
merge(array: &array, l:l, m:m, r:r)
}
}
func merge(array:inout [Int],l:Int, m:Int, r:Int) {
//创建两个子数组:L: a1[l..m] 和 a2: A[m+1..r]
let n1 = m - l + 1
let n2 = r - m
//数组赋值
let a1 = [Int](https://luowei.github.io/list/array[l ... m])
let a2 = [Int](https://luowei.github.io/list/array[m+1 ... r])
//var a1 = [Int](https://luowei.github.io/list/repeating: 0, count: n1)
//var a2 = [Int](https://luowei.github.io/list/repeating: 0, count: n2)
//var a1_i=0,a2_i=0
//while a1_i < n1 {
// a1[a1_i] = array[l+a1_i]
// a1_i+=1
//}
//while a2_i < n2 {
// a2[a2_i] = array[m+1+a2_i]
// a2_i+=1
//}
//合并两个子数组,重叠区间部分,用两个指针(i,j)轮换比较处理
var i=0,j=0,k=l
while i < n1 && j < n2 {
if a1[i] <= a2[j] {
array[k] = a1[i]
i+=1
}else{
array[k] = a2[j]
j+=1
}
k+=1
}
//超出区间部分追加上
while i < n1 {
array[k] = a1[i]
i+=1
k+=1
}
while j < n2 {
array[k] = a2[j]
j+=1
k+=1
}
}
//打印
func printMergeSortSort(_ array:inout [Int]){
mergeSort(array: &array, l: 0, r: array.count-1)
print(array)
}
var arr:[Int] = [3, 2, 5, 7, 1, 5, 4, 8, 11, 0]
printMergeSortSort(&arr)
Python实现
# MergeSort in Python
def mergeSort(array):
if len(array) > 1:
# r is the point where the array is divided into two subarrays
r = len(array)//2
L = array[:r]
M = array[r:]
# Sort the two halves
mergeSort(L)
mergeSort(M)
i = j = k = 0
# Until we reach either end of either L or M, pick larger among
# elements L and M and place them in the correct position at A[p..r]
while i < len(L) and j < len(M):
if L[i] < M[j]:
array[k] = L[i]
i += 1
else:
array[k] = M[j]
j += 1
k += 1
# When we run out of elements in either L or M,
# pick up the remaining elements and put in A[p..r]
while i < len(L):
array[k] = L[i]
i += 1
k += 1
while j < len(M):
array[k] = M[j]
j += 1
k += 1
# Print the array
def printList(array):
for i in range(len(array)):
print(array[i], end=" ")
print()
# Driver program
if __name__ == '__main__':
array = [6, 5, 12, 10, 9, 1]
mergeSort(array)
print("Sorted array is: ")
printList(array)
Java 实现
// Merge sort in Java
class MergeSort {
// Merge two subarrays L and M into arr
void merge(int arr[], int p, int q, int r) {
// Create L ← A[p..q] and M ← A[q+1..r]
int n1 = q - p + 1;
int n2 = r - q;
int L[] = new int[n1];
int M[] = new int[n2];
for (int i = 0; i < n1; i++)
L[i] = arr[p + i];
for (int j = 0; j < n2; j++)
M[j] = arr[q + 1 + j];
// Maintain current index of sub-arrays and main array
int i, j, k;
i = 0;
j = 0;
k = p;
// Until we reach either end of either L or M, pick larger among
// elements L and M and place them in the correct position at A[p..r]
while (i < n1 && j < n2) {
if (L[i] <= M[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = M[j];
j++;
}
k++;
}
// When we run out of elements in either L or M,
// pick up the remaining elements and put in A[p..r]
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = M[j];
j++;
k++;
}
}
// Divide the array into two subarrays, sort them and merge them
void mergeSort(int arr[], int l, int r) {
if (l < r) {
// m is the point where the array is divided into two subarrays
int m = (l + r) / 2;
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
// Merge the sorted subarrays
merge(arr, l, m, r);
}
}
// Print the array
static void printArray(int arr[]) {
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
// Driver program
public static void main(String args[]) {
int arr[] = { 6, 5, 12, 10, 9, 1 };
MergeSort ob = new MergeSort();
ob.mergeSort(arr, 0, arr.length - 1);
System.out.println("Sorted array:");
printArray(arr);
}
}
C 实现
// Merge sort in C
#include <stdio.h>
// Merge two subarrays L and M into arr
void merge(int arr[], int p, int q, int r) {
// Create L ← A[p..q] and M ← A[q+1..r]
int n1 = q - p + 1;
int n2 = r - q;
int L[n1], M[n2];
for (int i = 0; i < n1; i++)
L[i] = arr[p + i];
for (int j = 0; j < n2; j++)
M[j] = arr[q + 1 + j];
// Maintain current index of sub-arrays and main array
int i, j, k;
i = 0;
j = 0;
k = p;
// Until we reach either end of either L or M, pick larger among
// elements L and M and place them in the correct position at A[p..r]
while (i < n1 && j < n2) {
if (L[i] <= M[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = M[j];
j++;
}
k++;
}
// When we run out of elements in either L or M,
// pick up the remaining elements and put in A[p..r]
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = M[j];
j++;
k++;
}
}
// Divide the array into two subarrays, sort them and merge them
void mergeSort(int arr[], int l, int r) {
if (l < r) {
// m is the point where the array is divided into two subarrays
int m = l + (r - l) / 2;
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
// Merge the sorted subarrays
merge(arr, l, m, r);
}
}
// Print the array
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
// Driver program
int main() {
int arr[] = {6, 5, 12, 10, 9, 1};
int size = sizeof(arr) / sizeof(arr[0]);
mergeSort(arr, 0, size - 1);
printf("Sorted array: \n");
printArray(arr, size);
}
C++ 实现
// Merge sort in C++
#include <iostream>
using namespace std;
// Merge two subarrays L and M into arr
void merge(int arr[], int p, int q, int r) {
// Create L ← A[p..q] and M ← A[q+1..r]
int n1 = q - p + 1;
int n2 = r - q;
int L[n1], M[n2];
for (int i = 0; i < n1; i++)
L[i] = arr[p + i];
for (int j = 0; j < n2; j++)
M[j] = arr[q + 1 + j];
// Maintain current index of sub-arrays and main array
int i, j, k;
i = 0;
j = 0;
k = p;
// Until we reach either end of either L or M, pick larger among
// elements L and M and place them in the correct position at A[p..r]
while (i < n1 && j < n2) {
if (L[i] <= M[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = M[j];
j++;
}
k++;
}
// When we run out of elements in either L or M,
// pick up the remaining elements and put in A[p..r]
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = M[j];
j++;
k++;
}
}
// Divide the array into two subarrays, sort them and merge them
void mergeSort(int arr[], int l, int r) {
if (l < r) {
// m is the point where the array is divided into two subarrays
int m = l + (r - l) / 2;
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
// Merge the sorted subarrays
merge(arr, l, m, r);
}
}
// Print the array
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}
// Driver program
int main() {
int arr[] = {6, 5, 12, 10, 9, 1};
int size = sizeof(arr) / sizeof(arr[0]);
mergeSort(arr, 0, size - 1);
cout << "Sorted array: \n";
printArray(arr, size);
return 0;
}